The Planck's Radiation Formula Derivation Using the Einstein Coefficients

Some number of photons are assigned to every light wave having the frequency ν. Further, one assumes that there are discrete atomic (or molecular) energy levels.
 

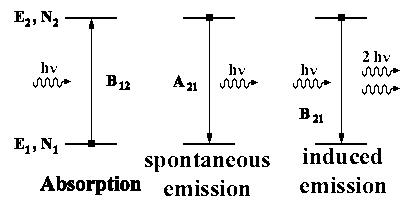hν  =  E2 - E1

•   Absorption of one photon hν causes an atom or molecule to go from the ground state E₁ to the excited state E₂. The number of absorption processes per unit time is proportional to the population number (?) N1 (number of the atoms / molecules in the lower state 1) and the radiation density u(ν). The probability of such a process occuring is given by the letter B12:

•  Emission of one photon hν = E₂ − E₁ corresponds to the transition from energetically higher state to the lower state. As with the absorption such a transition can be forced artificially. In this induced emission the number of photons increases and the population number (?) N2 decreases in time:

•  Spontaneous emission occurs from the state E₂, so that the population number N₂ (?) decreases:

Many transitions occur equally in both directions (absorption and emission) in the equilibrium position; therefore the population number (?) may not have any net change:

The coefficients A₁₂, B₁₂ and B₂₁ are determined from experiments: 

1.) For T ® ¥ should be u(ν) ® ¥.

2.) For small frequencies, hν << kT, should be hold true experimentally proven  Rayleigh-Jeans-Law {u(ν)  =  ^8pn²/_c³· kT}:
Series expansion: e^hν/kT » 1 + ^hν/_kT + ....    → u(ν) ≈  A₂₁/B₁₂  ^.kT/_hν

Comparing with the Rayleigh-Jeans-Law  gives:

The ν³ relation between spontaneous emission and absorption is very important here !
By combining what weve learned about the coefficients B₁₂, B₂₁ and A₂₁ ,we obtain the Planck Radiation formula:
 

Here we have also approached an important principle in the operation of Lasers; we must only interpret the above formula {^dN2/_dt = B₁₂ u(ν)N₁ − B₂₁ u(ν)N₂ − A₂₁N₂} in a different way:
Therefore we have laser operation when the photon production is alltogether more than 0. If u(ν) increases, N₂ should decrease, i.e. ^dN2/_dt < 0. This is important for the laser operation:

or if we neglect the spontaneous emission there will always be:

i.e. the population number (?) of the upper state should be more than the population number of the lower state. However this is not possible at thermal equilibrium position as one can see from examining the Boltzmann energy distribution. Thus lasers can be only operate in the non-equilibrium thermodynamic state.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.