Balls and Electrons![]()
Balls and Electrons![]()
A. Waves
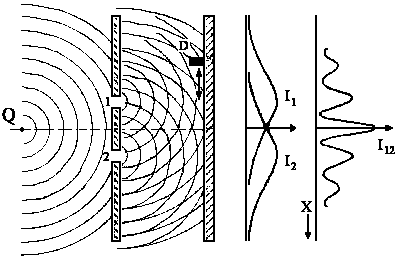 |
| Fig. 1: The diffraction of water waves |
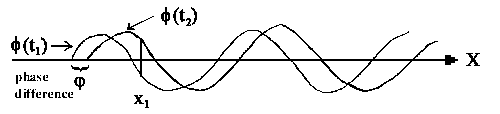 |
| Fig. 2: The distribution φ of wave in the x-direction for two times t1 und t2. |
Two water waves appear in figures 1 and 2 . These two waves interfere and are detected by the
detector D which gives a reading of the light intensity I. If we close one of the slits, we
will have only one wave. The sine-like wave that is produced should be recognizable to you. The distance between two wave crests (or two minimums) is called the
wavelength l. If we choose any point x on this wave,
this point vibrates as φ from t like a sine wave with the vibration
frequency v.
Detector D registers the Wave intensity I which is given
by I = |φ|2.
Next we open both slits and watch the waves φ1 and φ2 overlap in time. Both waves have the same
frequency. The overlapping of the waves causes a transitional shift which is described by the wave constant j (see figure 2). We have:
|
I = |φ1+φ2|2 |
A more precise equation for the intensity is
I = I1 + I2 + 2(I1I2)½.cos j. One can see
that intensity also oscillates with cos j. These
oscillations are especially strong for I1 = I2 =
I0, since then all the intensity swings between 0 and
4I0: I = 2I0·(1+cos j). We only have fourfold intensity in the most
extreme case. This is the case for each point x, however having
different phases in either point x.
B. Balls
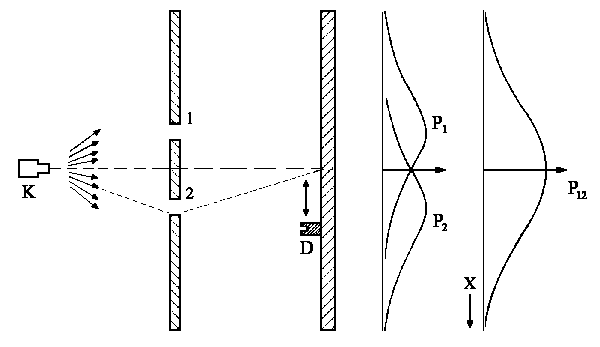 |
| Fig. 3: The experiment with balls. |
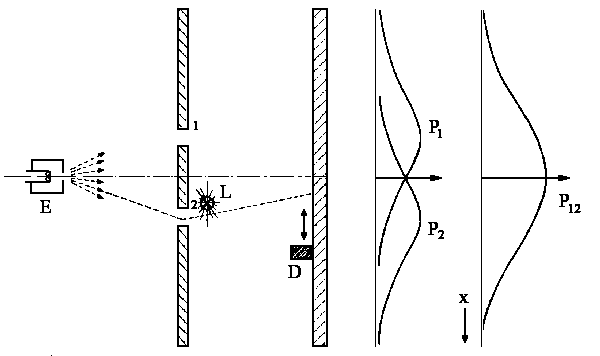
When we conduct the "Interference" experiment with balls, we can find the probability P1 of each ball passing
through slit 1 whether or not we keep slit 2 closed. We also can find the
probability P2 of each ball passing through slit 2 if we keep slit 1
closed. If the two slits are opened one can find the total probability which is
equal to:
| P12 = P1 + P2 |
 When the slits are situated far away from each other then
there is no total probability like the previous case and we will have the
individual probabilities P1 and P2. This scenario is displayed on the right in a more crude form:
When the slits are situated far away from each other then
there is no total probability like the previous case and we will have the
individual probabilities P1 and P2. This scenario is displayed on the right in a more crude form:
C. Electrons
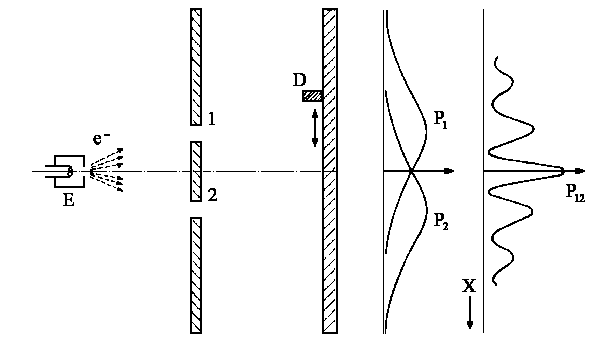 |
| Fig. 4: We will always have P12¹ P1+ P2, even in the case when we can only detect one electron at a time. |
In a similar experiment with electrons we learn that the total
probability P12 is not equal to the sum of particular probabilities.
This is the case even when we detect one electron at a time:
| P12 ¹ P1 + P2 |
The interference pattern which we observe on our screen corresponds to the
behavior of wave interference which we can easily describe. Next we can describe the result by applying two complex
numbers φ1 and φ2. The square of absolute
φ1 value gives the probability P1 whether slit 1 is
opened: P1 = |φ1|2. Similar to previous
statement one will have for slit 2 (when slit 1 is closed): P2 =
|φ2|2. And if both slits are opened however we will have
in this case:
| P12 = |φ1+φ2|2¹ |φ1|2 + |φ2|2 |
In order to describe our observations correctly we must use the mean of complex numbers in our calculations. In general, what will happen when we add a single electron that has passed through slit 1 or 2 ?
To get a result, we must carry out an experiment in which electrons
are observed together with the light source:
 |
| Fig. 5: Experiment with electrons that are passing through one slit which is lighted by a lamp. |
The observed electron distribution on the
screen matches exactly with the alternately closed slit. We have
| P12 = P1+P2 or P12 = |φ1|2+|φ2|2 |
Finally: If we carry out an experiment to determine the way an electron moves we can determine (with complete certainty) whether an electron took one path or another. The interference pattern disappears, however. If we aren't certain of the path of the electron then we can't say that it has taken by path 1 or 2. Consequently, we can't even be certain that an electron has passed through either slit.
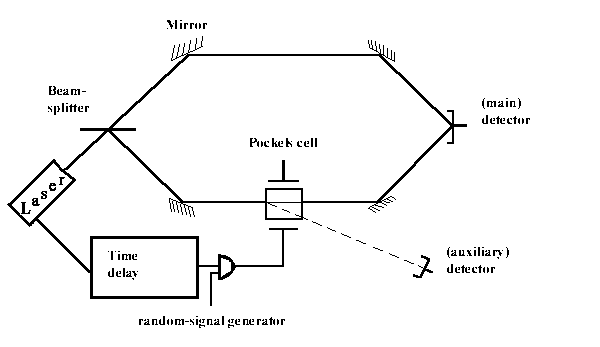
What will happen if an experimenter who is waiting for a particle to pass through the two slits decides to obtain measurements (and moreover the two slits are situated far away from each other)?
In this experiment the laser beam is directed on the beamsplitter and the split laser beams are collected by a detector which records the interference pattern. We can direct part of initial beam on the Pockels Cell. We can also direct photons on the auxiliary detector when applying different voltages. When we have zero voltage everything stays the same as it was before. The random-signal generator switches on the cell after the beam has passed the beamsplitter, but before it reaches the main detector. The photon can seemingly take either one way or the other. If the Pockels cell is turned off then we will see the interference pattern on the main detector.
This double-slit experiment shows that the two paths can be located as far away from each other as possible. The split beams can travel infinitely far in opposite directions before they combine with each other to produce an interference pattern.
Efforts with atoms
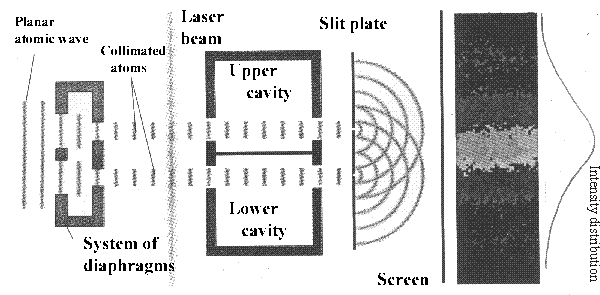 |
| Fig. 6: The double slit experiment features atoms passing through system of diagrams and a laser beam. Then atoms lose energy by falling to a lower energy level and producing photons which are stored in a cavity. Because this process doesn't influence atomic motion, we won't take the uncertainty principle into account here. Thus, this experiment shows that it is not possible to determine the path of atoms from the interference pattern. |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.