Let's expand our model of a particle in a one-dimensional potential well to a three-dimensional potential well which has the following size 0<x<a, 0<y<b, 0<z<c. Our particle, therefore, will have the following energy states:
E = h²/8m(n1²/a² + n2²/b² + n3²/c²)
where n1, n2 and n3 are quantum states along
x-, y- and z-axis correspondingly (ni = 1,2,3,...).
The
wavefunction y(x,y,z) = yx(x) . yy(y) ·yz(z) can be expanded as follows:
y(x,y,z) = (8/abc)½ .sin(n1πx/a) ·sin(n2πy/b) ·sin(n3πz/c)
If all well dimensions are the same, i.e. a = b = c then we have a unique situation because we can obtain the same energy values for different quantum numbers:
E = h²/8ma²(n12 + n22 + n32) = h²/8ma²· K2 = E1 · K2
Since we obtain the same energy values for different quantum numbers let's take some time to talk about state symmetry and degeneracy:
All combinations of n1, n2 and n3 that give the same K value have the same energy.
These same energy values are called degenerate energy levels. The
degeneracy degree, assigned as g, corresponds to the number of
independent wavefunctions which give the same energy. For instance, for the first six energy levels (where
E1 = h²/8ma):
| Energy | Combinations (n1, n2, n3) | Degeneracy g |
| 3 E1 | (1, 1, 1) | 1 |
| 6 E1 | (2, 1, 1), (1, 2, 1) (1, 1, 2) | 3 |
| 9 E1 | (2, 2, 1) (2, 1, 2) (1, 2, 2) | 3 |
| 11 E1 | (3, 1, 1) (1, 3, 1) (1, 1, 3) | 3 |
| 12 E1 | (2, 2, 2) | 1 |
| 14 E1 | (1, 2, 3) (1, 3, 2) ( 2, 3, 1) (2, 1, 3) ( 3, 1, 2) (3, 2, 1) |
6 |
The level degeneracy can always be explained by symmetry considerations. One can see the wavefunctions for a particle in two-dimensional potential well in the next illustration (see fig. 1).
yn1n2 =
(4/a b)½ sin(πx/a n1) ·
sin(πy/a
n2)
E = h²/8ma² (n12
+ n22)
For (n1 = 2; n2 = 1 and n1 =; n2
= 2) the energy levels are twofold degenerate. The wavefunctions y21 and y12
are asymmetric (i.e. they change its sign upon reflection relatively x-axis
(y21) and y-axis (y12)). Rotation by 90° transforms one
wavefunction into another.
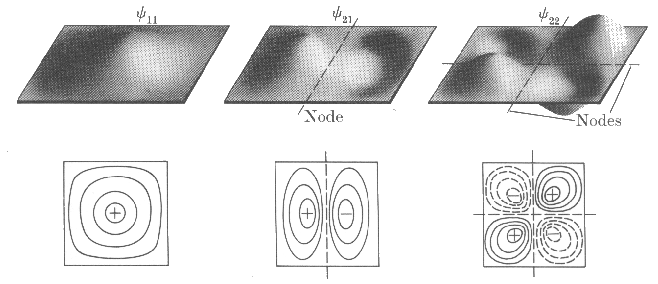 |
| Fig.1: Wavefunctions of a particle in two-dimensional potential well and its contour diagrams. |
If there is a symmetry point then the stationary levels are described by wavefunctions that have either positive (y(A) = +y(A')) or negative (y(A) = -y(A')) parity, i.e. the wavefunction sign either stays the same (positive parity) or changes (if coordinates reflect upon symmetry plane (for instance, x ®-x) when x = 0 is symmetry axis).
However: The difference in energy of adjacent levels is
higher when the wavefunction frequently changes its sign.
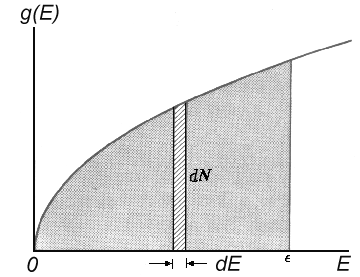 |
| Fig.2: The degeneracy density g(E) as a function of energy E. |
The particle which is squeezed in the the well can take only definite
discrete energy values. It's quite easy to calculate
the state numbers d N(E) in the range [E, E + dE] and then find the energy state
density g(E) = dN/dE, i.e. the amount
of states per range of energy unit:
| g(E) = 2πV(2m³)½/h³. E½ |
And then one can obtain the state sum Q from which it's also possible to
derive all other thermodynamical quantities:
| Q = V/h³ (2πmkT)3/2 |
Moreover we've received a very important quantity: number of state transitions.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.