The Simple Molecular Vibrations:
The Harmonic Oscillator


The potential energy of a diatomic molecule has a minimum energy when the atoms are separated by some defined distance.  The potential energy V(x) expansion in series relative to state of equilibrium x0(for which                        dV(x)/dx|x0 = 0 ) gives V(x) = V(0) + ½ d²V(x)/dx²|x0 x2. If we choose the zero point of energy V(0) and assign d²V(x)/dx²|x0 as constant k then we obtain the potential approximation

V(x)  =  ½ kx²          (x is a value that corresponds to deviation from equilibrium position)

The Schroedinger equation 

(−h²/2md²/dx² + ½ kx²) y  =  E y

Since A and B vibrate in the opposite directions then we will change m to reduced mass µ = mAmB/mA+mB. If we introduce a new distance variable quantity          z² = x² (kµ/h²)½  then we finally obtain the Schroedinger equation:

(−d²/dz² + z²) y(z)  = 2 E/hw·y(z)

where the vibration frequency is as follows w  =  (k/µ)½ . A reader who is interested in more detailed mathematical solution can find it here.


Result:

Generally it's considered for possible energy levels:
 

En  =  hw (n + ½)

where n can take the following values n = 0, 1, 2, .... .

The energy ground state Eo = ½ hw is assigned as the zero point energy. The wavefunction of this lowest energy state is the Gauss function:

yo(z)  = p-¼ e−z²/2

The highest possibility of the system being in the ground state can be found at z=0, or equilibrium. In general one can obtain for the wavefunction of n-state
 

yn(z)  =  Cn Hn(z) e−z²/2

where constants Cn can be obtained from the normalization condition -¥ò+∞yn* yn dz = 1 in the following way:
 

Cn  =  1/(π½n!2n )½

and the functions Hn(z) are the Hermitian polynomials:
 

H0(z)  =  1
H1(z)  =  2z
H2(z)  =  4z2 − 2
H3(z)  =  8z3 − 12z
H4(z)  =  16z4 − 48z2 + 12
H5(z)  =  32z5 − 160z3 + 120z
H6(z)  =  64z6 - 480z4 + 720z2 − 120


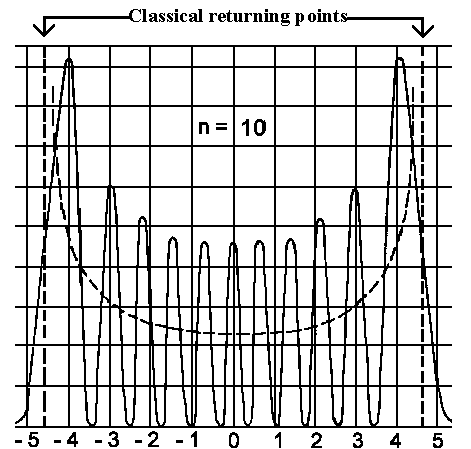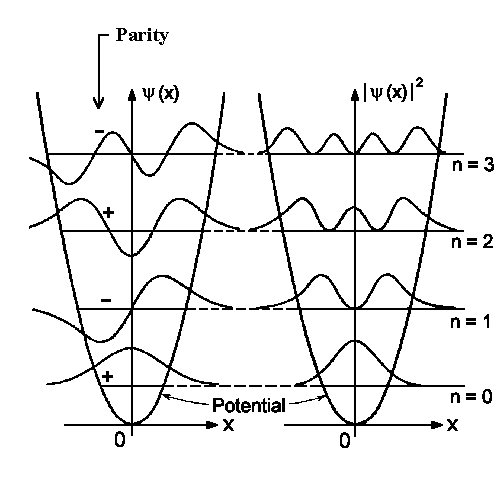
This natural quantum number of vibrations is assigned by v in the spectroscopy (against assignment by n) and therefore the energy levels are as follows                   Ev = hw (v + ½) where v = 0,1,2,... . And nothing changes by its meaning, that's for sure!

 
The wavefunction (to the left) and the detection probability (to the right) for four lowest vibrational states.  The detection probability for the vibrational state n=10. The dashed line gives us the classical detection probability.

The highest probability of locating the particle in the ground state is in the equilibrium position. The quantity |yn|2 would be higher in the classical turning points region E = V(x).
The dependence of classical oscillator detection probability is given by 1/w(xm²−x²)½. This curve (see dashed line on the right illustration) is assigned to probability density in the range [x, x+dx]; i.e. the highest chance is in the classical turning points xm. One can find that quantum description converges with the classical description for higher states.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.