The harmonic oscillator for which the restoring force F is proportional to the deviation of x from the equilibrium position can be described by the potential energy V(x). Since F ~ −d/dxV(x) the potential energy can be written as follows:
V(x) = ½ kx²
And the Hamiltonian operator and the Schroedinger equation:
(−h²/2µd²/dx² +
½ kx²) y = E y
where µ is the reduced mass. Since we want to be as brief as possible, we will introduce new
variables z² = x²(kµ/h²)½ and ε = E/h(µ/k)½ = E/hw
with [w = (k/µ)½] and finally obtain (d²/dx² =
(kµ/h²)½d²/dz²):
½ (−d²/dz² + z²) y(z) = E/hw = ε · y(z)
= H y(z)
One who is not interested in the mathematical derication can go to the link here to see the final result.
Now we want to factorize the term (−d²/dz² + z²) as for instance −a² +
b² = (−a + b) (a + b). It's not so easy for the operator because we must pay
attention to the precise consequence. And we produce for check
| 1/Ö2(−d/dz + z) | 1/Ö2(d/dz + z) |
| |¾¾¯¾¾¾| | |¾¾¾¯¾¾| |
| a+ | a− |
a+a− y(z) = ½ (−d²/dz² + z²) y(z) + ½(−d/dz z + z d/dz)y(z)
where ½ (−d²/dz² + z²) = H and Hy = e y one can obtain:
a+a− y = ey + ½ (-y(z) − z d/dzy + z d/dzy) = (e-½)y
Now it's the equation for the harmonic oscillator.Let's now try to calculate the permutation relation between a− and a+:
[a−, a+] = a−a+− a+a− = ½[(d/dz + z) (−d/dz + z) − (−d/dz + z) (d/dz + z)] y
= ½ [−d²/dz²− z d/dz + d/dz z + z² + d²/dz²² − z d/dz + d/dz z − z²] y = [−z d/dzy + d/dz (z y)] = y
| a−a+ − a+a− = 1 |
Applying a− to our equation a+a− y = (ε −½)y :
a−a+ a-y = (e- ½) a-y
(a−a+ )(a-y) = (e- ½) (a-y)
(a+a− + 1) (a-y) = (e- ½)(a-y)
a+a− (a-y) = (e- 3/2)(a-y)
By applying the operator a− to our wavefunction ywe obtain the wavefunction (a−y) that is enough for our harmonic oscillator equation a+a-y = (ε − ½) y, for the eigenvalue which is smaller than about 1: (e- ½) → (e-3/2). The operator a− decreases the eigenvalue on 1 and therefore it's also called the annihilation operator.
Since ε is the measure of energy E (ε = E/hw)
then it should be the lowest state yo. If we
apply the annihilation operator to yo then
we cannot obtain more deep state. This is not possible! And finally it's
considered for the lowest state
a− yo = 0 and εo-½ = 0
| εo = ½→
Eo = ½ |
The lowest energy state has the energy ½hw. And calculating the corresponding wavefunction one can
obtain:
a− yo = (d/dz + z) yo = 0 → dyo/dz = −z yo → dyo/yo = −zdz → ln yo = Co' e−z²/2
| yo = Co e−z²/2 |
Co can be obtained from normalization condition -¥ò+∞yo* yo dz = 1 in the following way:
Co = p-¼
And now applying a+ to our equation a+a-y = (ε − ½) y:
a+ (a+a-)y = (e- ½) a+y
a+ (a−a+− 1) y = (e-½) a+y
a+a− (a+y) = (ε + ½)(a+y)
The application of a+ to y increases the
eigenvalue on about 1. Therefore a+ is also called the
production operator. If we apply a+ to the lowest state yo then we will obtain the wavefunction y1 that is the eigenfunction closer to the higher
eigenvalue:
| y1 = a+yo |
y1 = C1 (−d/dz + z) · e−z²/2
y1 = C1 2z · e−z²/2
y2 = a+y1 = C2 (−d/dz + z) z · e−z²/2
y2 = C2(2z² − 1) e−z²/2
E2 = 5/2hw
and so on.
Generally one can obtain for any n-wavefunction yn
yn = Cn (a+)n yo
In general one can write down the following formula for possible energy
values:
| En = |
The ground state energy level Eo = ½
hw is the zero point of energy.
Generally one can obtain for the wavefunction of n-state
| yn(z) = Cn Hn(z) e−z²/2 |
where the constant Cn can be obtained from the normalization
condition -¥ò+∞yn*
yn dz = 1:
| Cn = 1/(π½n!2n )½ |
and the function Hn(z) is the Hermitian polynomial:
| H0(z) = 1 |
| H1(z) = 2z |
| H2(z) = 4z2 − 2 |
| H3(z) = 8z3 − 12z |
| H4(z) = 16z4 − 48z2 + 12 |
| H5(z) = 32z5 − 160z3 + 120z |
| H6(z) = 64z6 - 480z4 + 720z2 − 120 |
All other polynomials can be obtained from the recursion formula
| Hn(z) = 2z Hn−1(z) − 2(n−1) Hn−2(z) |
for instance in order to obtain H3(z) one must do the following Hn−1(z) ® H2(z) and Hn−2(z) ® H1(z):
H3(z) = 2z · (4z2−2)− 2(2) (2z) =
8z3 − 12z
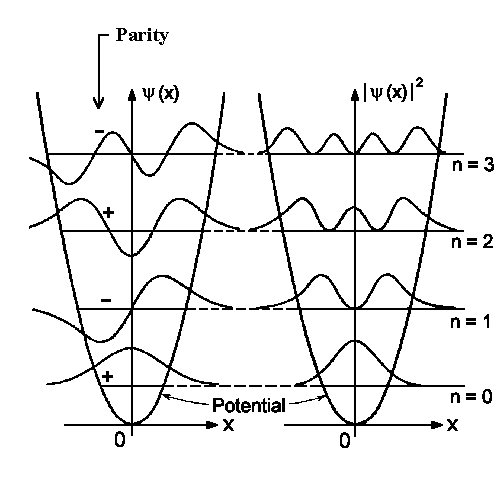 |
|
Fig. 1: Four lowest wavefunctions and its probability density for the harmonic oscillator. |
![\includegraphics[angle=-90,width=0.9\textwidth]{graphs/osz_properbility.eps}](../../PC3/Kap_III/img40.gif) The highest
detection probability in the ground state is in the equilibrium position (see
Fig. 1 for n=0). When increasing vibrations the quantity |yn|2 would be higher for classical
turning points E = V(x); see figure to the left for n=5, 10, 20.
The highest
detection probability in the ground state is in the equilibrium position (see
Fig. 1 for n=0). When increasing vibrations the quantity |yn|2 would be higher for classical
turning points E = V(x); see figure to the left for n=5, 10, 20.
How much does the probability density for the classical oscillator in the range [x, x+dx]?
Classical oscillator: x = xm sinwt xm = maximum deviation
In the time interval dt (in which one observes the particle) the deviation dx will be as follows:
dx/dt = xmwcoswt
dt = dx/xmw coswt = dx/xmw (1−sin²wt)½
dt = dx/w (xm²−x²)½
The quantity 1/w(xm²−x²)½ shows the probability density to find particle in the range [x, x+dx]; i.e. the highest chance to detect particle is in the classical turning points xm.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.