The Tunneling Phenomenon

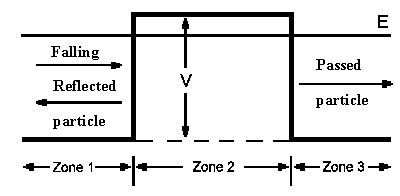
Let's consider a particle with mass m which is moving with energy E (from left side) toward a potential energy barrier having width a. It's easy to predict what will happen in the classical mehanical case: if particle energy E is smaller than barrier height V then the particle will be reflected. Only in the case when E is greater than V will the particle pass through the barrier. Quantum mechanics gives us an ambiguous answer. To find the answer, the Schroedinger equation must be divided into 3 different equations, each of which applies to one one of the three zones shown in the diagram. The solutions of the three equations in the transition regions must be continuous with each other. This must also be true for the steps (first derivatives) of the wavefunctions. The ratio of squared probability amplitude for a paricle moving to the right and a particle moving to the left gives the transmission probability T  (Derivation):
 

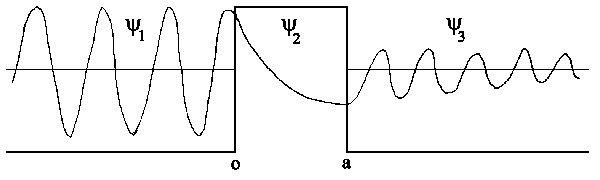
Although E < V the transmission probability T isn't equal to 0, i.e. a particle can cross the potential barrier that wouldnt be allowed in classical physics. The wavefunction isn't equal to 0 at point x=0 since V is finite in height and width. One can write the following approximation for ka > 1:
 

One can see the tunneling probability T against different energies E and constant potential barrier V on the next figure. Where the idealized fragmentation potential of H in H-N₃ was chosen in a way that H-N₃ would be in excited state.

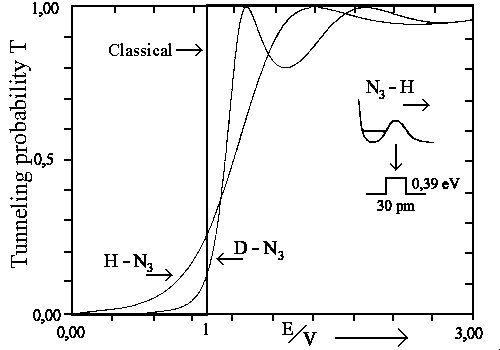The tunneling probability (idealized case) for H-N3 and D-N3 in the excited states. Classically T = 0 for E/V<1 and T = 1 for E/V>1.

The potential width is 30 pm and its height is V = 0,39 eV ≡ 37,6 ^kJ/_mol. The tunneling probability strongly depends on mass as one can see from replacement of H into D.

The technical application of tunneling phenomenon is Rastertunnelmicroscop.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.