of the Hydrogen Atom
The starting point of our talk is the ODE for R(r) that we obtained before the derivation of the squared kinetic moment eigenfunction Yl,m(J,j):
[−h²/2µ 1/r² ∂/∂r(r² ∂/∂r) + V(r) +
h²l(l+1)/2µr²− E]
R(r) = 0
One can write the following V(r) = −Ze²/4peo1/r for the potential of Z-electrons revolving around
nucleus. Multiplication by −2µ/h gives us:
d²/dr² R + 2/r dR/dr +
[2µE/h² + 2µ/h²Ze²/4peo1/r−l(l+1)/r²] R = 0
To shorten our last equation, we introduce a few abbreviations and a new radial wavefunction which is assigned by a prime (R' ≡d R/dr ):
ρ = 2 ε r
B = Ze²µ/4peoh²ε ε² =
−2µE/h²
(binding energy)
| R'' + 2/ρ R' − [¼−B/ρ + l(l+1)/r ²] R = 0 |
For high distances (ρ →∞) there are no 1/r ,1/r ² -terms:
R'' − R/4≈ 0 → R(ρ) = C e−ρ/2 or R(ρ) = C e+ρ/2
The second solution is given up since R(ρ) isn't limited for high distances
and would be infinite.
The more detailed solution is given elsewhere
but we write the short form with the solution here:
If we have a look at the ODE and compare coefficients at ρk (ODE should be true for any r and hence for any ρk) we will obtain:
ak+1/ak = l + k + 1 −B/(k + 1) (k + 2l + 2)
The series begins with k = 0. They should finish somewhere in order to stop
R-increasing, i.e. one of the coefficients should be 0:
| l + k + 1 | − B = 0 |
| ½¾¯¾½ | |
| n |
l, k, 1 are integer numbers, i.e. n = l + k + 1 should be also
integer
| n = 1, 2, 3, 4 ...
0 ≤ l ≤ n −1 |
where l, k = 0, 1, 2, 3....
n is the main quantum number |
Introducing B = n we can shorten our equation:
| En =
−µ/2(Ze²/4peo |
So the energy is quantized according to the main quantum numbers n and the possible values of kinetic moment are l = 0, 1, 2, ..., n−1 and there are (2l+1) m-values for each l.
For n = 1: l = 0, k = 0 → R(ρ) = C e−ρ/2
or after introduction of r = (2Z/aon) r : R(r) = C e−Zr/nao
with the following abbreviation (Bohr radius)
ao = 4peoh²/µe²
The polynomial S akρk in the obtained solution R(ρ) = e−ρ/2.ρlΣk=0 akρk is also referred to as associated Laquere polynomial (Σk=0 akρk ≡ Ln-l-12l+1(ρ)). There can be confusion with the Laguere polynomials because they are defined differently in some other textbooks. We will use the mathematical which is used in the "Mathematica" toolbox. This approach can be used to calculate any Laguerre polynomial (Rodrigues representation):
It's very simple for any Mathematica user. The following program string gives
you back first five associated Laguerre polynomials:
Do[Print[ "n=",n,"
l=",l," " ,
LaguerreL[n-l-1,2l+1,x]],{n,1,5},{l,0,n-1}]
The table
of polynomials for low level electrons shows they are really simple functions:
| Electron | n | l | Ln-1-12l+1 (x) |
|
2 p 3 d 4 f |
1 2 3 4 |
0 1 2 3 |
1 1 1 1 |
| 2 s 3 p 4 d |
2 3 4 |
0 1 2 |
2 - x 4 - x 6 - x |
| 3 s 4 p |
3 4 |
0 1 |
6 - 6x + x² 20 - 10x + x² |
| 4 s | 4 | 0 | 24 - 36x + 12x² - x³ |
The total solution for the radial part of wavefunction is then as follows
| Rn,l = cn,l ·ρl. e−ρ/2 Ln-1-12l+1(ρ) |
where the constant cn,l is also the normalization factor.
It can be obtained from the normalization condition:
| oò¥ Rn,l · Rn,l · r² dr = 1 |
If we now substitute ρ with r using r =
(2Z/aon)
r then we will obtain the following total solution:
| Rn,l = -{4(n−l−1)! Z³/[(n+l)!]n4ao³}½ (2Zr/nao)l e−Zr/nao Ln-l-12l+1(2Zr/nao) |
where
| ao = 2 r Z/n ρ =
|
The wavefunctions Rn,l(r) and probability to detect an
electron at the distance r from nucleus
Rn,l2r2 are shown on the next two
figures:
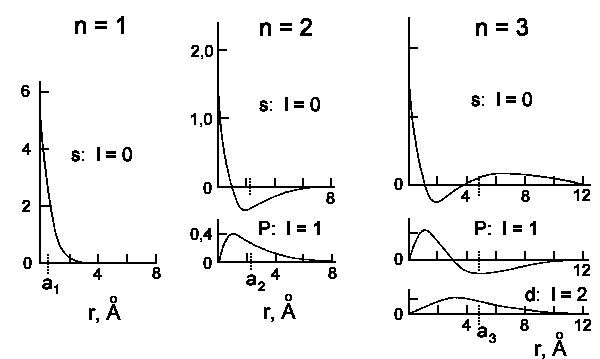 |
| Radial wavefunction of hydrogen atom for n = 1, 2 and 3. The ordinate
is always [Rn,l(r) m−3/2]·10−8. |
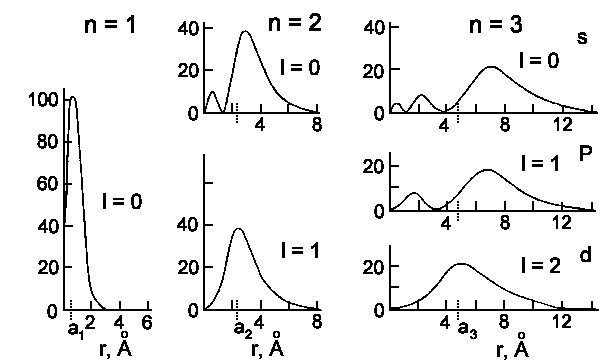 |
| Radial detection probability in the hydrogen atom for n = 1, 2, and 3.
The ordinate is always [e² Rn,l²(r) · 10−15. |
The
obtained images of all wavefunctions y(r,J,j) = R(r) .Y(J,j)
for hydrogen-like atoms are given in the next chapter.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.