Optical Transitions

The light emission produced in optical transitions is not described using quantum mechanics here. Instead we use a half-classical estimation in a common approximation. The vibrating dipole sends electromagnetic waves in classical electrodynamics.  The dipole in the following mathematical description is the dipole moment:
 

  = − e · (charge · distance [C · m])

where  is the vector coming from (+)charge to a vibrating (-)charge. According to the "Conversion table" we can transform classical quantity into quantum mechanical operator (→µ) obtaining average of distribution

<µ>  =  òy*() (− e) y() dV

for any optical transition.

[Atom or molecule has a diameter of about few Angströms; the light in thevisual wavelength range is about 5000 Å. According to bigger scale of wave compare with atomic or molecular sizes the electrical force of the field doesn't change in an atomic or molecular spatial range.]
 

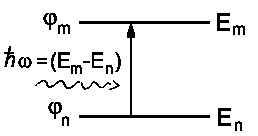What, however, are the wavefunctions y*, y ? If we consider our atom with both energy levels En and Em and corresponding wavefunctions jn and jm then y() is the time overlapping of these both functions in a  time- dependent form:

y(,t)  =  1/Ö2[jn() e−iEnt/h + jm() e−iEmt/h]

(Since light is an electromagnetic radiation that vibrates in time, we must  time t into our future considerations. 1/Ö2 is only for normalization).

Average of distribution calculation <µmn(,t)>:
 

<µmn>  =  1/2 ∫(jn* eiEnt/h + jm* eiEmt/h)(−e)(jn e−iEnt/h + jm e−iEmt/h) dV
=  −e/2{ ∫jn* jn dV + òjm* jm dV +   òjn* jme−i(Em−En)t/h dV + òjm* jne+i(Em−En)t/hdV}
             |¾¾¾¾¾¾¾¯¾¾¾¾¾¾¾|
            time-independent		   |¾¾¾¾¾¾¾¾¾¾¾¾¯¾¾¾¾¾¾¾¾¾¾¾¾¾¾| 
time-dependent

The time-independent part vanishes for even and odd wavefunctions j since |j|² is even (|j()|²  =  |j(-)|²) . Multiplication by and then integration over the whole volume gives us 0.

Using the following short form w = (Em− En)/h we see the dipole moment distribution average vibrates as a classical dipole and produces an electromagnetic field:
 

 <µmn> = ( −e òjm* .. jn dV eiwt   +  complex conjugate ) / 2

As we will see later, only the squared |<µmn>|² is relevant for all rearrangments in experiment so that the complex conjugate part gives the same contribution as the first part of the formula. Now we would like to introduce the following  abbreviation:

Rmn= òjm*  jm dV

which will finally gives: 

<µmn> =  -e Rmn eiwt

If the above-mentioned integral Rmn vanishes, the transition is forbidden (the forbidden electrical dipole transition). The calculation of dipole matrix elements plays a key role in optical transition calculations.

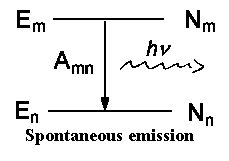
An atom or molecule in the excited energy state Em moves into lower energy state En while emitting light simultaneously.  An ensemble of excited atoms (or molecules) emits light independently from one another. The radiation energy Smn over time or volume for these spontaneous transitions is as follows:
 

Smn  =  Nm  hνmn Amn
Energy flux density / Jm-3s-1 ­ ­   ­ ­Transition probability for spontaneous emission / s-1
  ·   Energy difference Em− En ≡ Energy of Photons / J
 Particle density in an excited state / m-3

The transition probability Amn [s-1] of making quantum mechanical calculations and transforming some relations from electrodynamics into quantum mechanics will be given below. We have already found that energy flux density S is as follows (in electrodynamics): 

S  =  4/3. Nm/c³. 1/4peo. <|d²µ/dt²|²>t

where brackets <>t are for time mean value of time-variable quantity (here one can see the second time derivative of dipole moment). The quantum mechanical dipole moment average of distribution is <µmn> = −eRmneiwt from which we can easily obtain the quantum mean value by using 2-fold derivation:

<|d²µ/dt²|²>t  =  |e Rmn w² eiwt|²  =  (2π)4νmn4 e² |Rmn|²

®      Smn  =   4/3. Nm/c³. 1/4peo· 16π4 νmn4 e² |Rmn|²


Smn  =  16π³/3. e²/eoc³. νmn4|Rmn|² · Nm
=  Nm hνmn Amn
Amn  =  8π²e²/3heoc³ . νmn³ |Rmn|²

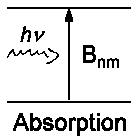
There are induced processes which are caused by light influence on a particle along with spontaneous emission that is characterized by Amn and is independent of the external field of radiation. 
 

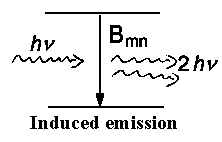The corresponding coefficients Bnm for absorption and Bmn for induced emission have been already given. The relations between them are as follows:
 

Amn/Bmn  =  8πhν³/c³ and Bnm/Bmn  =  gm/gn

where gm and gn  show the degeneracy of corresponding energy levels. If degeneracies are equal we will have:
 

Bnm  =  Bmn

The first equation represents an important ν³-ratio between spontaneous and induced emission; the second equation shows that probabilities are the same for induced emission and (induced) absorption. 
Readers can find more about lasers in "Spektrum der Wissenschaften": Anwendungen des Lasers, ISBN: 3-922508-47
The relation with Rmn:

Bmn  =  e²/6eoh² |Rmn|²

 

The transition moment can also be represented by the so-called oscillator force f (this name came from the classical way of measuring an electron that is vibrating freely in three dimensions, with a mass me possesses an oscillator force f = 1):
 

fmn  =  4p nmnme/3h |Rmn|²

The oscillator force f is dimensionless. The intensive transitions have typical oscillator forces laying in the range between 0,1 and 1. The forbidden transitions lay lower f ≈10-5.
 

The transition moment µmn , Rmn and fmn are theoretical quantities; but what do we measure in experiments and how do we come to these theoretical quantities? The answer is given here!



Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.