Entwicklungssatz

Allgemein läßt sich jede Funktion in eine Reihe nach einen vollständigen Satz von Funktionen entwickeln:
 

y(x) = åi ci φi(x)
(Die φi sollen orthonormal sein)

Zur Bestimmung aller Koeffizienten ci in der Reihenentwicklung wird von links mit Fk* multipliziert und über den gesamten Raum integriert.

ò fk*(x) y(x) dx = åi ci òfk*φidx = ck

Der sehr abstrakte Entwicklungssatz, dass sich jede Funktion in eine Reihe mit einem vollständigen Satz von Funktion entwickeln läßt, ist von fundamentaler Bedeutung für die Chemie.
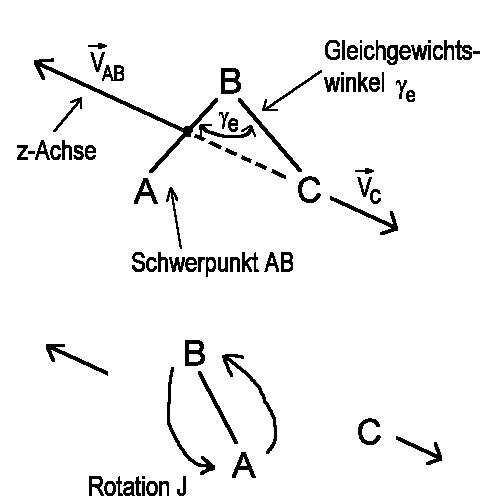Abb.1: Einfacher Bindungsbruch eines dreiatomigen Moleküls, ABC.
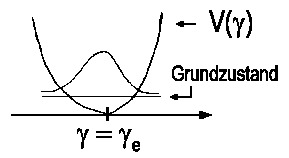Abb.2: Schwingungsgrundzustand (Biegeschwingung) des dreiatomigen Muttermoleküls ABC

Betrachten wir z. B. den Zerfall eines dreiatomigen Moleküls ABC in das Molekül AB und das Atom C, wobei die ursprüngliche Bindung B-C einfach "wegfallen" soll, d. h. man stelle sich anschaulich B-C durch eine "Stange" fest verbunden vor, die dann entfernt werden soll. Ohne auf eine detaillierte quantenmechanische Beschreibung einzugehen, kann man sich vorstellen, dass die Wellenfunktion, die den Grundzustand des Muttermoleküls (also die Situation vor dem Zerfall) beschreibt, sich in den Produkten wiederfinden muss, da sich ja bis auf eine Veränderung der Ortskoordinate R, die den relativen Abstand der beiden Produkte beschreibt, nichts geändert hat  (Abb. 1).
Wir stellen also die ursprüngliche Wellenfunktion des Grundzustandes y(G) (Abb. 2) durch Terme der Produktwellenfunktion φ(P) dar:

y(G) = åk ck φ(P)

Die Koeffizienten ck erhält man durch Berechnung von

ck = ò fk(P)* y(G) dV

Diese Berechnung, übertragen auf den Zerfallsprozeß, bei dem das Produkt AB rotieren soll, bedeutet nichts anderes als die Grundzustandswellenfunktion y(G)nach den Rotationseigenfunktionen zu entwickeln. Da der Zerfall in der Ebene stattfinden soll, sind die Rotoreigenfunktion unsere Kugelflächenfunktionen Yl,m=0(J,j).Die Funktion y(G) soll nun nur den für den Zerfall wichtigen Teil, nämlich die Knickschwingung um den Gleichgewichtswinkel γe, beschreiben.
Für den niedrigsten Schwingungszustand wird die Wellenfunktion durch eine Gaußkurve y(G)(γ) ~ exp[-α(γ-γe)2] beschrieben (s. Abbildung), wie wir es aus der Behandlung des harmonischen Oszillators kennen. Wir wollen nun noch die Nomenklatur für die speziellen Yl,m=0 hier ändern und sie YJ(γ) nennen; dann sind die Entwicklungskoeffizienten gegeben durch :

cJ =  ò YJ(γ) exp[-α(γ-γe)2] sinγ dγ            (sinγ dγ = dV)

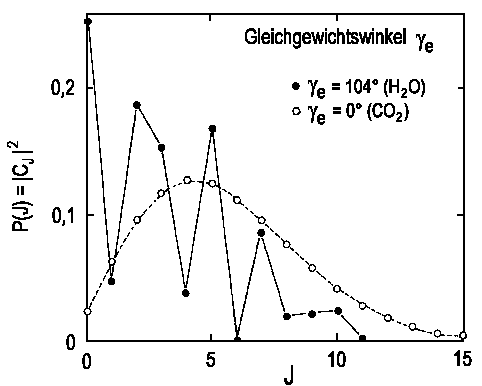
Die Wahrscheinlichkeit, eine bestimmte Rotation vorzufinden, ist gegeben durch P(J)=|cJ|2.

In der unteren Abbildung sind die so berechneten Verteilungen für H2O ® OH(J)+H und CO2® CO(J)+O angegeben. Die dazu benötigten Integrale sind lösbar, man muss lediglich γe und a kennen, die vom jeweiligen Molekül abhängen (Gleichgewichtswinkel γe ist über die Molekülstruktur gegeben und αläßt sich über die Knickschwingungsfrequenz berechnen).






Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.