von Wasser
Man kann die irreduzible Darstellung von Normalschwingungen eines Moleküles analog zu der der Molekülorbitale bestimmen. Dazu muss die Symmetriepunktgruppe des Moleküles ermittelt werden um deren Symmetrieoperationen anschließend einzeln auf die Schwingung anzuwenden. Für jede Symmetrieoperation ist zu entscheiden, ob sich das Vorzeichen der Bewegungsvektoren der einzelnen Atome durch die Symmetrieoperation ändert oder nicht. Wir wollen dies anhand der Normalschwingungen des Wassermoleküles demonstrieren. Das Wassermolekül ist folgendermaßen orientiert:
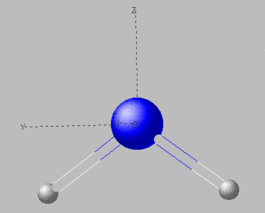
Das Molekül liegt in der yz-Ebene und die z-Achse bildet die Winkelhalbierende des H-O-H-Winkels (Hauptdrehachse). Die cartesischen Koordinaten der Atome lauten wie folgt:
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
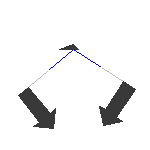
Trägt man die Bewegung der einzelnen Atome in die Struktur als
Vektoren ein erhält man folgende Bilder:
| Knick
1960 cm-1 |
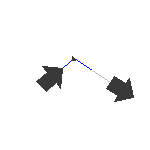
asymm. Streck
4084 cm-1 |
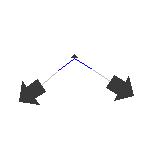
symm. Streck
4049 cm-1 |
|---|---|---|
 |
 |
 |
| als VRML
7589 Bytes
als AVI 109920 Bytes |
als VRML
7545 Bytes
als AVI 109936 Bytes |
als VRML
7552 Bytes
als AVI 109934 Bytes |
Für Wasser (Symmetriepunktgruppe C2v) ergibt sich folgende Charakterentafel:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wir bestimmen zunächst die irreduzible Darstellung für die
Knickschwingung (1960 cm-1). Für die Indentität ergibt
sich 1, da sich nichts ändert.
| E | C2 | sv | sv' |
|---|---|---|---|
| 1 |
Bei der Drehung um die z-Achse (C2) ergibt sich keine Vorzeichenänderung für die Bewegungsvektoren (ergibt 1 in der Charakterentafel).
| E | C2 | sv | s'v |
|---|---|---|---|
| 1 | 1 |
Für die Spiegelung sowohl an der xz-Ebene, als auch an der yz-Ebene gilt das selbe (keine Vorzeichenänderung der Bewegung svektoren, eine 1 in der Charakterentafen).
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
Vergleicht man das Ergebnis der Betrachtung mit der Charakterentafel,
so erhält man für die Knickschwingung die irreduzible Darstellung A1.
Für die symmetrische Schwingung ergibt sich nach dem selben Schema ebenfalls das Mulliken-Symbol A1, da keine Symmetrieoperation
das Vorzeichen ändert.
Für die antisymmetrische Schwingung tritt hinsichtlich einer Spiegelung an der xz-Ebene und hinsichtlich der Drehung um C2 eine Vorzeichenänderung auf und wir erhalten das Mulliken-Symbole
B2.
|
|
Energie/cm-1 |
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
An dieser Stelle sei eine Warnung ausgesprochen. Häufig wird das Wassermolekül nicht wie in Abb.1 dargestellt in die yz-Ebene (sondern in die xz-Ebene) gelegt, dann werden die σv und die σv'-Ebene für die Bestimmung der elektronischen Zustände und für die Bestimmung der vibronischen Zustände entgegengesetzt definiert. Das hat dann zur Folge, dass ein B2 zum B1 wird und umgekehrt.
Die Schwingungen wurden mit der MNDO-Methode berechnet. Als Ergebnis
erhält man die Eigenwerte (Schwingungswellenzahlen) und die Eigenvektoren
geben die Bewegung der einzelnen Atome in den drei Raumrichtungen an.
| Wellenzahl (cm-1) | H | O | H | |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.