Harmonic Oscillator

Introduction

Many physical systems, such as a weight suspended with a spring, experience a linear restoring force when displaced from their equilibrium position. The mathematical expression for such a restoring force, F, is:

F  =  −kx

k is a proportionality constant called the force constant and x is the displacement from the equilibrium position. This relationship is called Hooke's law. For the spring example, k will be large for a stiff spring and smaller for springs that are weaker. Similarly, if you stretch a spring twice as far, it "springs back" with twice the force. Of course this law is valid for limited values of x. Try stretching a spring too far and you'll find that the restoring force is no longer directly proportional to displacement!

The potential energy, V, for a one-dimensional system is equal to the negative of the force integrated over x:

V(x)  =  -òFdx  =  k∫ xdx  =  ½ kx² + constant

The constant of integration depends on the physical system being modeled. For the ground state of a diatomic molecule, as modeled below, we can set it to zero.

Harmonic Oscillator Model for a Diatomic Molecule

We can model the bond in a molecule as a spring connecting two atoms and use the harmonic oscillator expression to describe the potential energy for the periodic vibration of the atoms. The potential energy, V(x), of a particle moving in one dimension is given by:

V(x)  =  ½ kx²

where k is the force constant as above and the constant of integration is zero. We can make this expression more useful by changing x to R-Re, where R is the internuclear distance (the distance between atoms) and Re is the equilibrium internuclear distance (the bond length):

V(R)  =  ½ k(R − Re)²

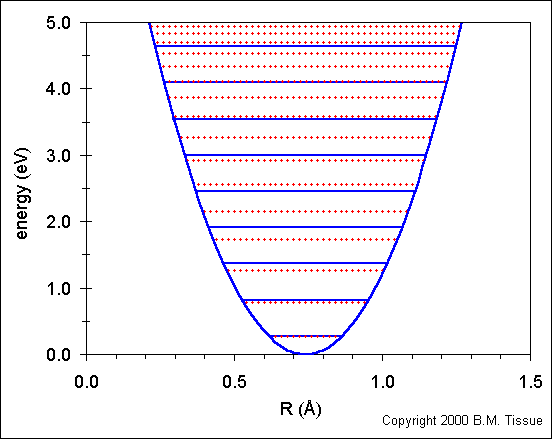
The following figure shows the ground-state potential energy curve (called a potential well) for the H2 molecule using the harmonic oscillator model. Re for H2 is 0.7412 Å. There is one obvious deficiency in the model, it does not show the energy at which the two atoms dissociate, which occurs at 4.748 eV for the H2 molecule (1 eV = 8065.48 cm-1). At some internuclear distance the atoms are far enough apart so that they do not "feel" each other. That is, they are isolated and the bond is broken. A more realistic model of the potential well of a diatomic molecule is the Morse potential, which does model the dissociation energy.

harmonic oscillator energies

The solid blue horizontal lines show the energy levels that are calculated using the harmonic oscillator model:

Ev  =  (v + ½) νe

where v is the vibrational quantum number (v = 0,1,2,...). The v = 0 level is the vibrational ground state and is the lowest horizontal line in the plot.

νe is called the vibrational constant:

νe  =  ½ πc  Ö(k/m)

where µ is the reduced mass (m1m2/m1+m2). The simple harmonic oscillator provides a good fit to energies for the lowest energy levels, but fails at higher energies.
The dotted red lines shows the energy levels calculated from:

Ev  =  (v + ½) νe− (v + ½)² νexe + (v + ½)³ νeye + higher terms

where v and νe are the same as above and xe and ye are the first and second anharmonicity constants respectively. These correction terms provide much better match of the calculated energies to the energies that are observed experimentally.
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.