Wave Function Expansion

In general, it is possible to replace any wave function by a complete series of eigenfunctions:  

For determination of all coefficients c_i in the expansion series, the equation above is multiplied from the left side with φ_k* and then integrated within space.

Wave function expansion, a very abstract approach, is of fundamental importance in chemistry.

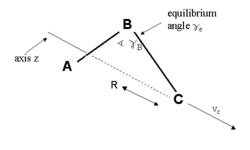
Fig.1: Simple breakage of bond within the three atomic molecule ABC

For example, consider the decomposition of the three atomic molecule ABC that yields molecule AB and atom C. Assume that the bond B-C simply disappears. Without going into a detailed description in quantum mechanical terms, it is possible to imagine that the wave function that describes the ground state of the parental molecule (i.e. the situation prior to decomposition) is as well represented by the products as there is only a change in the coordinate R which represents the distance between the two products (Fig.1).

Thus, we replace the original wave function for the ground state ψ^(G) (Fig.2) by wave functions representing the products φ^(P):

The coefficients c_k are calculated using

This calculation, transferred to the process of the molecule's decomposition, is identical to an approach where the ground state wave function Ψ^(G) is obtained by expanding the rotational eigenfunctions. As decomposition shall take place in a planar system, the spheric surface function Y_l,m=0(θ,φ) represents the rotational eigenfunctions. Function ψ^(G) is confined to the aspect relevant for decomposition, i.e. the bending mode vibration around the angle of equilibrium γ_e.

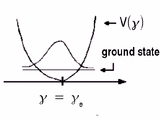Fig.2: Normal mode of vibration (bending) of the parent molecule ABC

In analogy with our mathematical treatment of the harmonic oscillator in its lowest vibrational state, the wave function of interest has gaussian characteristics (comp. Fig.2).

Having replaced Y_{l,m =0} by Y_J(γ); the expansion coefficients are obtained from:

with sin γdγ = dV.

The probability to observe are certain rotational state is given by

The diagram below depicts the calculated distribution for H₂O → OH(J) + H and CO₂ → CO(J)+O. It is possible to solve the necessary integrals for known values of &gamma_eα. Note that the molecular structure defines the equilibrium angle γ_e and the value for α can be calculated from the frequency found for the bending mode of molecular vibration.

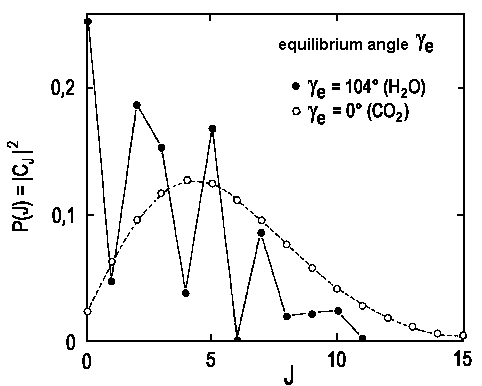Fig.3: The relative number of product molecules in the rotational states J. The theoretical treatment assumes that the ground state vibrational energy is completely transferred in rotational energy of the diatomic product. (filled dots for OH, empty dots for CO).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.