The LCAO method adopts an especially simple form for homonuclear diatomic molecules, i.e. molecules that consist of two identical atoms, e.g. H2, O2, N2. It is recommendable to begin with the most simple among those systems, the hydrogen molecule ion H2+. As this molecule has only one electron, this molecule is for a consideration of the chemical bond as fundamental as the hydrogen atom for the structur of the atoms of the periodic table of elements.
Keep in mind that αA and αB in both secular equations have identical values as there is no difference between the two ends of the molecule and an electron hat the same energy in φA (around nucleus A) as in φB (around nucleus B). In consequence, we take αA = αB = α and obtain the following secular equations:
| cA(α − E) + cB(β − ES) = 0
cA(β − ES) + cB(α − E) = 0 |
As solutions relevant (i.e. cA and cB are not zero) to our problem (derivation) we obtain
| E± = [α± β]/[1±S] |
The easiest solution to the problem is
| E± ≈ α ± β |
for values of S small in comparison to 1. For "slightly larger" values of S the equation E± ≈ α ± (β − αS) represents a good approximation.
The equations show the way a formerly degenerated pair of energy values α splits symmetrically in two values below and above the original energy. It is as well recognizable that the extent of the splitting is determined by the value of (β - αS). The MO with the lowest energy is called the bonding MO. Its energy is below the energy of the hydrogen atom and represents the ground state of the molecule. The other MO with the higher energy is the antibonding MO which is higher in energy than the hydrogen atom. The results are depicted schematically in the following figure. The only situation where we get an asymmetric splitting is for values of S that are not neglectable when compared with 1.
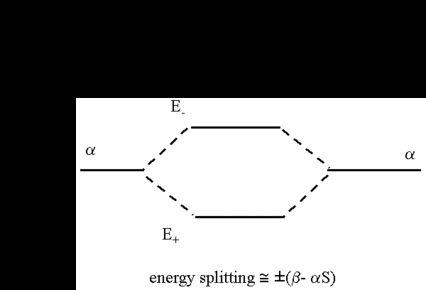
To determine the wave function ψ = cAφA + cBφB for the energy levels, we need the coefficients cA and cB. By inserting both energy values E± into the secular equation, we obtain the two solutions for cA = ± cB. For the respective molecular orbitals we get:
| ψ+ = cA (φA + φB)
ψ− = cA (φA − φB) |
with a coefficient cA that is determined in the usual way by normalization.
| ψ+ = (φA + φB) / √[2(1+S)]
&psi− = (φA − φB) / √[2(1−S)] |
The obtained wave functions Ψ+ and Ψ- as well as the square of their absolute values |ψ+|² and |ψ-|² for the ion H2+ are depicted here.
Before proceeding our calculation, we substitute φA and φB with the atomic orbital 1s of the hydrogen atom. Now we are able to calculate α, β and S for any distance R between the two nuclei. Thus, we obtain the electronic energy. The sum of this energy and the energy e²/(4πεoR) emerging from the repulsion between the nuclei represents the total energy of the molecule.
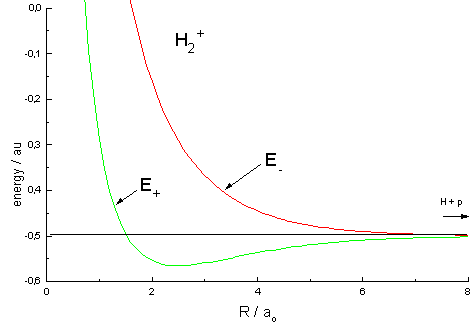 |
| Fig.1 Curves representing the total energy for the bonding (+) and the antibonding (-) MO as a function of the internuclear distance R.
Atomic units used: ao = Bohr's radius, energy unit au is twice the ionization energy of the hydrogen atom. |
The energy curves for ψ+ and ψ- reveal the following properties of the ion H2+
Energy curves of this type are called "attractive" and "repulsive" and the respective molecular orbitals "bonding" and "antibonding". These terms already correspond to molecular dynamics and in fact, the experimental finding is that a hydrogen ion H2+, having absorbed the energy necessary for lifting the electron from the bonding into the antibonding orbital, dissociates:
H2+ + hν → H + H+
![]()
Complementary Mathematics on the Ion H2+
As we deal with one electron and the presence of this particle is spreaded over space, 1 is the value of the following integral:
∫|ψ+|2 = 1 = ∫ cA(φA+φB)·cA(φA+ φB) = cA2 (∫|φA|2 + ∫2|φAφB| + ∫ |φB|2)
With the known values of the integrals (∫|φA|2 = ∫ |φB|2 = 1) and the with ∫2|φAφB| = 2S
we get the coefficients and the wave functions for the molecular orbitals.
| bonding: | cA2 = 1/[2(1+S)] | ψ+ = (φA + φB) /√[2(1+S)] |
| antibonding: | cA2 = 1/[2(1-S)] | ψ- = (φA − φB) /√[2(1-S)] |
The density probabiliy P therefore is (|φA|2+2|φAφB| +|φB|2) / [2(1+S)]. I.e., the density of the electrons charge per nucleus is 1/[2(1+S)] and 1/(1+S) for an electron that is assigned to both nuclei and thus regarded as bond.
Users of Mathematica are free to get an impression of the respective functions Ψ+ / Ψ-, resp. the square of their absolute values |Ψ+|² and |Ψ-|². In addition, the dependency of these functions on the internuclear distance Rgl can be plotted:
Rgl=2.4;
psiP=Exp[-Sqrt[x^2+y^2]/2]+Exp[-Sqrt[(x-Rgl)^2+y^2]/2]
psiM=Exp[-Sqrt[x^2+y^2]/2]-Exp[-Sqrt[(x-Rgl)^2+y^2]/2]
Plot3D[psiM, {x,-4,6}, {y,-4,4},PlotPoints -> 50, PlotRange -> All]
Plot3D[psiP, {x,-4,6}, {y,-4,4},PlotPoints -> 50, PlotRange -> All]
Plot3D[psiP^2, {x,-4,6},{y,-4,4}, PlotPoints -> 50, PlotRange -> All]
Plot3D[psiM^2, {x,-4,6},{y,-4,4}, PlotPoints -> 100, PlotRange -> All]
The Hamiltonian operator of the molecule ion H2+ is:
H
=
−h²
/2mΔ + e/4πεo
[ - 1/rA
- 1/rB
+ 1/R]
or, in the so-called atomic unit au:
H = − ½Δ − 1/rA - 1/rB + 1/R
Our treatment of hydrogen yielded the following expression for the ground state energy of this atom in atomic units au
(-½Δ - 1/rA) φA = - ½ φA
Using the equations for the Hamilton operator and the value for the hydrogen atom we obtain the following energy term J:α = ∫φA*HφAdτ
with H φA = (-½Δ − 1/rA − 1/rB + 1/R) φA = - ½ φA + (-1/rB + 1/R)φAα = -½ +∫φA* (- 1/rB + 1/R)φAdτ = -½ + J
where J is the so-called Coulomb integral J = - ∫φA* · 1/rB · φAdτ + 1/R
Using the equations we obtain as well the energy terms K and S:ß = ∫φB* HφAdτ = -½ ∫φB*φAdτ + ∫ φB* (- 1/rB + 1/R)φAdτ = -½ S + K
where K is the resonance integral K = - ∫φB* 1/rBφAdτ + S/R
and where S is the overlap integral S = - ∫φB*φAdτ
| E± = [α± β]/[1±S] = -½ + [J±K]/[1±S] |
For 1s orbitals, we obtain:
S = e-R (1 + R + 1/3·R2)
J = e-2R (1 + 1/R)
K = S/R - e-R(1 + R) = e-R[1/R - 2/3R]
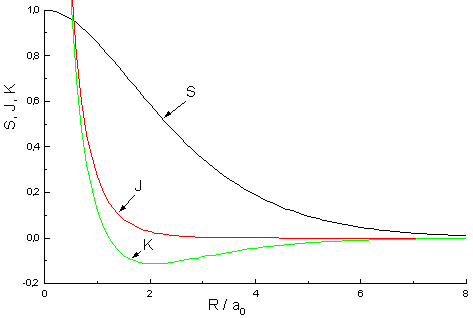 |
| Fig.2: Dependency of Overlap integral S, coulomb integral J and resonance integral K from the internuclear distance R |
The minimum for E+ is found easily by setting the derivative to zero and resolving the equation for R:
DEpl=D[Epl,R];
FindRoot[DEpl==0,{R,{1.5,2.5}}]
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.