Laser technology is based on
Light Amplification by Stimulated Emission of Radiation
.
 |
 |
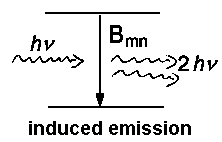 |
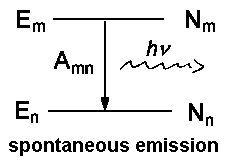
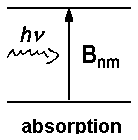
| Fig. 1: Spontaneous and induced incidents between a higher energy level m and a lower level n. Nm or Nn respectively denotes the number of atoms or molecules in the level. | ||
With u(ν) as the spectral radiation density (details here ), the relative numbers of spontaneous to induced emission for thermal equilibrium is given by:
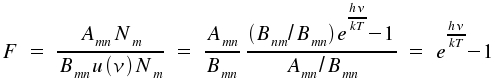
Within the visible range of the electromagnetic spectrum, e.g. for green light with a wavelength of λ = 500 nm = c ⋅&nu-1 and a temperature of 300 Kelvin, this ratio becomes F = e96 = 5⋅1041. Therefore, among 5⋅1041 incidents, only one is due to induced emission.
In contrast, for the microwave range with frequency ν = 1 GHz = 109 Hz and the same temperature the expected ratio F is 1.6⋅10-4. Therefore, nearly all incidents are induced. For a wavelength of 60 &my;m, spontaneous and induced processes contribute to the same (F = 1) extent to emission. Thus, it is not astonishing that the first laser produced microwaves. In the respective publication of 1954 by Townes et al., the experimental setup is described as NH3-Maser. By the way, masers have existed for millions of years in the universe, especially in regions where new stars are formed. So far, OH-, H2O- and an SiO-maser have been observed. The reaction H2O (hν < 190 nm) → OH + H or collisions occuring in specific states come into question as the source for OH.
|
Independent from the construction in detail, lasers are characterised by two energy levels. The number of species in the higher energy level exceeds the one in the lower level. Therefore all lasers have three components in common (Fig. 2):
|
 |
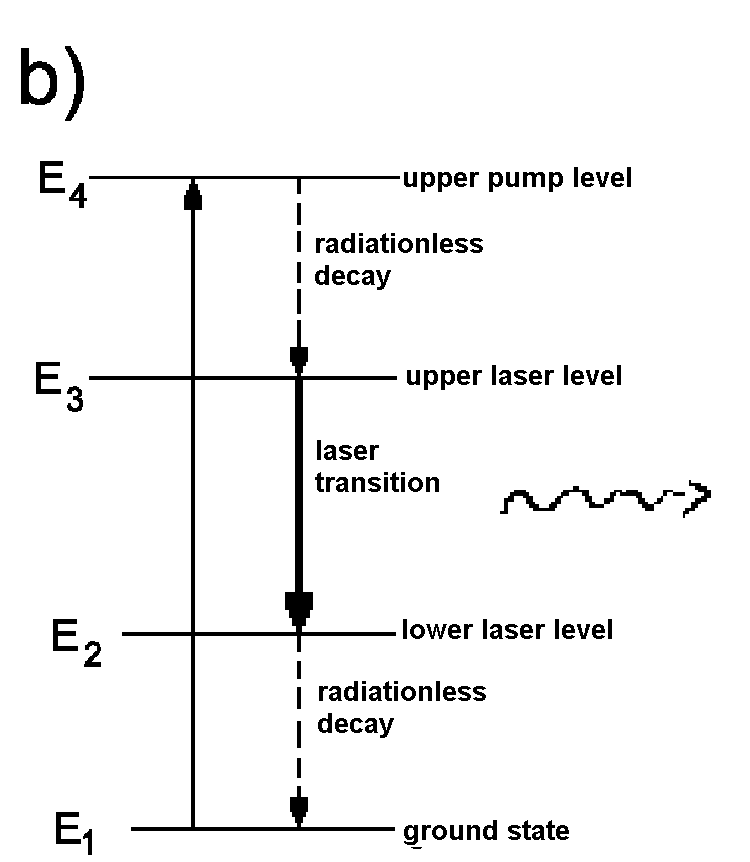 |
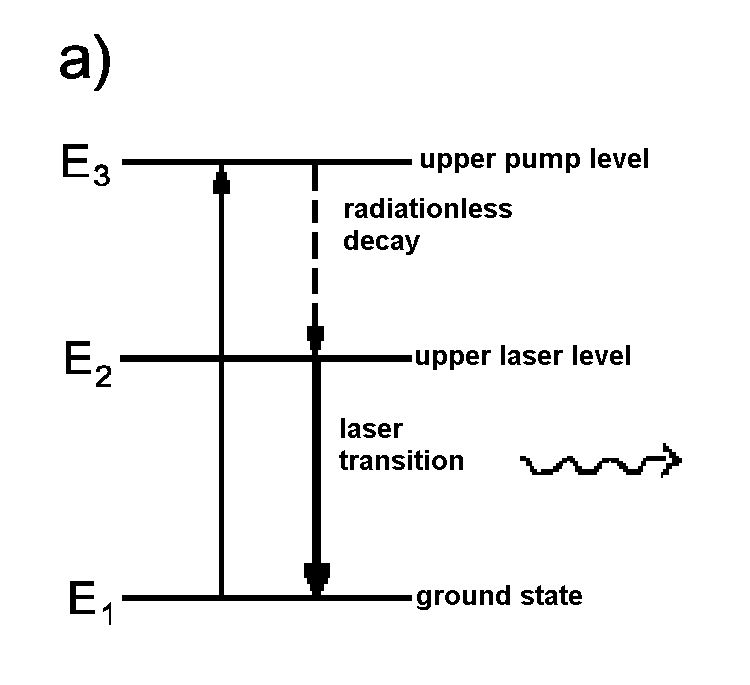
| Fig. 3:To realize an overpopulation of the upper energy level, at least three energy levels have to be present in the medium within laser cavity. a) Three level principle of a ruby laser, b) Four level principle. | |
The first laser system developed by Maiman in 1960 was a ruby laser based on the three level principle. Nowadays, the four level principle is fundamental for almost all lasers systems as, with this principle, a weakly populated lower energy level is easier to realize.
The properties of laser light:
Monochromatic (coherence respective time)
Non divergent (spatial coherence)
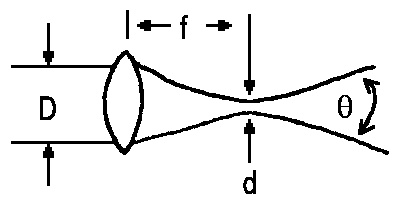
Using a lens, it is possible to focus a laser beam on a spot of diameter d.
Here, f denotes the focal distance of the lens. As, for the best lenses, the ratio of focal lens to diameter is about 0.8, it is a rule of thumb that half the wavelength is the lower limit of the diameter of the spot.
Short light pulses:
High power output
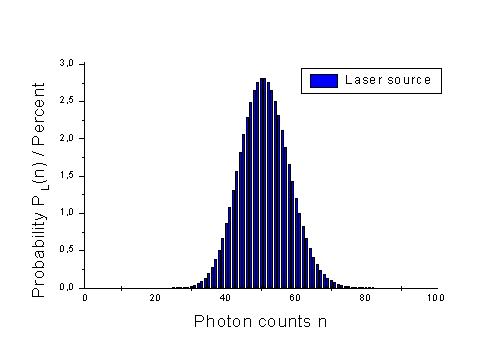
Photon statistics
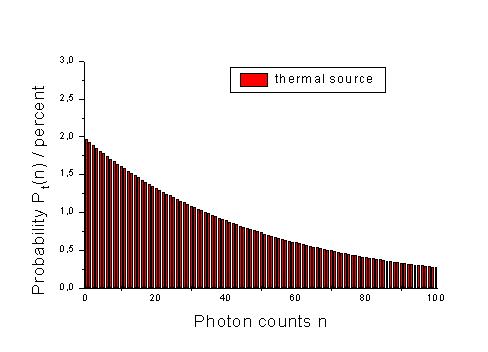
For thermal sources, this probability is decribed by the following distribution.
In contrast, for light emerging a laser, the probability distribution Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
Laser light is confined to a narrow band Δν around the frequency νL. (Hänsch was able to reach a ratio Δν/νL≈ 10-15). Therefore, lasers are used to to adjust high resolution spectroscopic appliances.
Due to coupling of the molecules or atoms within the resonator, an almost not divergent beam of light of diameter D is obtained. Ideally, the uncertainty principle is the limiting factor for the angle with which the beam widens.
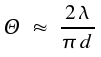
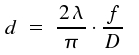
Due to certain technical arrangements (Q-switch, coupled modes, pulse compression), the generation of light pulses of some nanoseconds duration is possible. (6 femtoseconds have been reached). This allows to observe chemical reactions in real-time.
In continous action, energy transformation rate of CO2 lasers is around
Assume a light source and a volumen element in which photons emitted by this source are counted. The probability for the case of detecting n photons is P(n). This probabiliy is shown for a thermal source of light and a laser source. (Here, <n> is the middle number of photons in our statistical approach, i.e. 50 photons for the 101 cases with n = 0 as the minimal number of photons and n = 100 as maximal number of photons.)
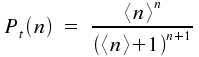
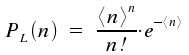
![]()