Classification of molecules
according to symmetry

If analysis of a molecule yielded a list of all present symmetry elements, such a list is the basis to form classes of molecules with common symmetry. Such a class is called a symmetry point group. Any molecule is unambiguously a member of one single point group. Though the point groups relevant in chemistry are numerous, we are able to work straightforward within this field as these groups are characterized by sets of increasingly complicated symmetry operations.
Two notations are in use, the Schönflies system (according to Arthur Moritz Schönflies, 17.4.1853 - 27.5.1928). and the Hermann-Mauguin system. The former is more common in the discussion of individual molecules, the latter is used almost exclusively in the discussion of crystal symmetry. Note that both are expressions of one single system and they only differ with respect to semantics.
List of point groups
-
The groups C1, Ci and Cs. If a molecule (or any object) possesses no symmetry element other than the identity, it belongs to Ci. Only a rotation about 360° produces an identical image of the molecule. As this operation establishes the initial orientation, any body, asymmetric as it may be, meets this criterion. If a molecules possesses the identity and the inversion as the only elements, it belongs to the group Ci. If it possesses a plane of symmetry as the only element apart from the identity, it is classified as belonging to the group Cs.
-
The groups Cn. If a molecule possesses the identity element and an n-fold axis of symmetry, it belongs to the group Cn. (Note that Cn is now playing a triple role: it is a label for one of the symmetry elements present and denotes the corresponding operation as well as the name of the group.)
-
The groups Cnv. Objects in these groups possess a Cn axis and n vertical reflection planes σv.
-
The groups Cnh. Objects possessing a Cn-axis and a perpendicular horizontal mirror plane belong to the group Cnh. Note that this is an example for a group where automatically other symmetry operations can be applied. In this case the inversion i is found too as C2 and σh are present.
-
The groups Dn with molecules possessing an n-fold principal axis and n two-fold axis perpendicular to Cn.
-
The groups Dnh. Molecules belong to this group if they belong to Dn and possess a horizontal mirror plane. All homonuclear diatomics belong to group D∞n and all heteronuclear molecules to C∞v.
-
The groups Dnd. The classification of Dn is also based on Dn but requires the additional presence of vertical mirror planes bisecting the angles between all the neighbouring axis C2.
-
The groups Sn. Molecules with an rotatory reflection axis Sn belong to this group. There are only a few molecules with n < 4. Group S2 is identical with Ci.
-
The cubic groups T and O. A number of very important molecules possess more than one principal axis of symmetry. For example, CH4 possesses four C3 axes, one along each bond. The groups to which these belong are called the tetrahedral groups T, Td and Th and the octahedral groups Oh and O. The regular tetrahedron is a representative of Td; the regular octahedron of Oh. If the molecule possesses the rotational symmetry of the tetrahedron or the octahedron but none of its planes of reflection, it belongs to the simpler groups T and O, respectively. The group Th is slightly peculiar because it is based on T but also includes a centre of inversion.
-
The full rotation group R3 is the group of operations shown by a spherical object. An atom belongs to R3, but no molecule does. Exploring the consequences of R3 symmetry is a very important way of applying the group-theoretical arguments to atoms.
A flow chart flow chart provides valuable help in the classification of molecules.
Examples:
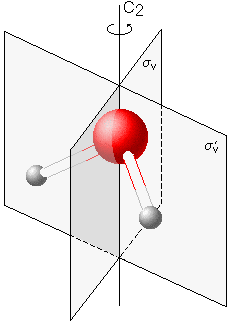 |
Water
The water molecule possesses one two-fold rotational axis C2
and two mirror planes σv and σ'v parallel to this axis. Therefore, it belongs to symmetry point group C2v. |
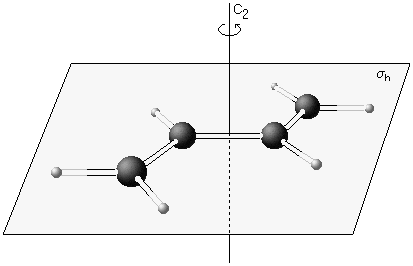 |
trans-Butadiene
This molecule possesses a centre of inversion i, one two-fold rotational axis C2 and a mirror plane σh which is horizontal, i.e. perpendicular to the axis. Trans-butadiene falls in symmetry point group C2h. |
|
|
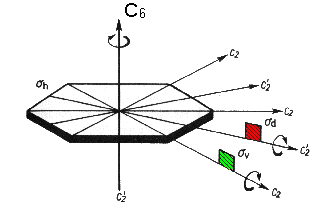 |
Benzene
The features of this molecule are a centre of inversion i, rotational axes C2 and C2' and C6, a horizontal mirror plane σh perpendicular to C6 and mirror planes σv and σd parallel to C6. This leads to a classification in point group D6h. |

 Contents
Contents 
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]()



![]()