Groups and their representations

Explanation of the term "group"

In general, molecules and crystals possess not only one but several symmetry elements. Thereby, not any combination is possible. If, for example, there is a mirror plane and a rotational axis, the latter cannot slant; either it has parallel or perpendicular orientation. This exemplifies that symmetry elements do not exist independently from each other but are linked with each other. The group, one of the most important terms in modern mathematics relates them. Without the symmetry operation of translation left aside, possible combinations are called point groups, a term underlining the simplicity of these combinations where one point or one axis plays a special role as being part of all symmetry elements, i.e. axes and planes,

The set of symmetry elements of a molecule determines its symmetry and is subsumed in a group. Certain conditions have to be fulfilled to use this term. Elements of a group can be combined in a way that

1. if A and B are elements of one group (do not mix with the Mulliken symbol), a combination A · B yields an element C which is as well found within the group.
2. In any group, the identity element E is present. For combinations of E with any element, commutivity E · B = B · E = B is found.
3. Combinations within the group are associative so that the combination A · B · C is equivalent to (A · B) · C and A · (B · C)
4. For any element of the group, there is a so-called inverse element denoted with a superscript of -1. Combinations between element and inverse element produce the identity element E. In mathematical terms A · A^-1=  A^-1 · A = E.

In our context of symmetry operations, there is a combinations of group elements called "multiplication". The product A · B denotes that symmetry operation B is first applied to the molecule and that the obtained positions of nuclei are submitted to operation A. In total, the effect is identical to performing C on the initial molecule. Note that the sequence of operations is of relevance, no commutivity law of the kind B · A = A · B is valid. In cases where these four conditions or "group axioms" are kept, an ensemble of elements represents a group. The number of elements in a group is called the group's order.

Example NH₃
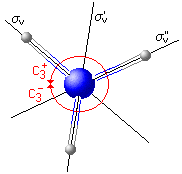
Some of the fundamental considerations in group theory are presented for ammonia. For this molecule, E, C₃⁺, C₃^-, σ_v, σ_v' and σ_v" are symmetry operations, therefore the molecule NH₃ belongs the the group C_3v.

	C3+	anti-clockwise rotation around the vertical 3-fold axis
	C3-	clockwise rotation around the 3-fold axis C3 (Movie, 455kB)
	σv	reflection on vertical plane σv (Movie, 393kB)
	σv'	reflection on vertical plane σv'
	σv"	reflection on vertical plane σv"

As mentioned above, sequential application of certain symmetry operations yields some other symmetry operations of the same group. Such combinations are denoted as a product of two operations, i.e. E = C₃⁻C₃⁺ means that the molecule is first rotated anticlockwise (C₃⁺) and then clockwise (C₃⁻) as, by convention, the operation on the right side is the first to be performed. Figure 1. below demonstrates the effect of an exchanged position within the product. Apparently, the final positions of the hydrogen atoms differ.

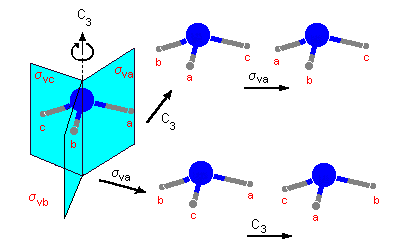Fig. 1: The two results obtained for applying a pair of symmetry operations in two different orders to the ammonia molecule.

From forming pairs of the six symmetry operations found for the molecule NH₃, we get a total of thirty-six products. The so-called multiplication table represents all possible combinations. Note that the element within the column is the first and the element in the row is the second to be performed. With respect to A · B as a representation of the product, the first factor A relates to the row and the second factor B to the column.

It is as well possible to represent the transformations by a multiplication of matrices. A general introduction of how a point with the coordinates (x,y,z) is transformed is found here. A multiplication of two matrices yields another matrix which represents some symmetry operation too. For example, the expression D(σ_v)D(C₃⁺) = D(σ_v")  fits exactly with the multiplication σ_vC₃⁺= σ_v".
A set of the six matrices which represent the symmetry operations of the group C_3v is called the matrix representation of the group C_3v.

  Contents  

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.