Rotatory-reflection S_n

Another operation that yields an image which is identical to the original is a combination of rotation and reflection. The body is turned by 360°/n about an axis and then submitted to reflection on a plane perpendicular to the axis. With the same result, the reflection can be performed first and the rotation second. This symmetry operation is called a rotatory-reflection and the symmetry element is an n-fold rotatory-reflection axis. The symbol S_n denotes the symmetry operation as well as the symmetry element. Neither the involved axis nor the plane need to be symmetry elements for themselves. The values for n in rotatory-reflection S_n are even numbers or 1.

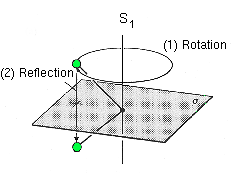
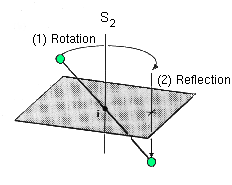
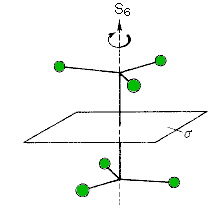
Rotatory-reflection axes Sn with n = 1, 2 and 6. - For S1 we have the special case of an ordinary reflection on a horizontal plane and - S2 equals inversion i.

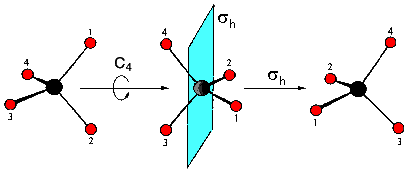
Example 1: Rotatory-reflection S₄ of the molecule CH₄ (Movie, 1.2 MByte)
 

Example 2: SiF₄

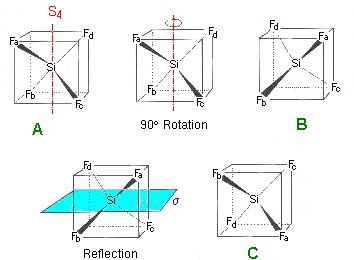
SiF₄ possesses four axes C₃ . There is no axis C₄ but a rotatory-reflection axis S₄.
 

Example 3: trans-1,2 Dichlorethen
 

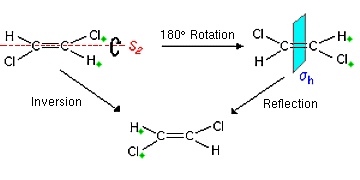
If the molecule trans-1,2 Dichlorethen is turned about 180° around the CC-σ-bond and subsequently reflected, a rotary-reflection is performed. The axis S₂ runs through both carbon atoms. As mentioned above, the symmetry elements S₂ ≡ i and σ ≡ S₁.

  Contents  

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.