of Water
Like with molecular orbitals, it is possible to determine the irreducible representation of the normal vibrational modes. For that purpose, it is first necessary to determine the point group of the molecules. Then, any symmetry operation of that group is applied to the vibrational modes. The motion vector for that vibration will be inverted or not affected. We now want to demonstrate this for the water molecule. The figure below defines the molecule's orientation:
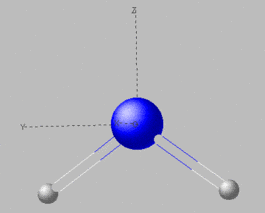 The molecule lies within the plane yz and axis z which bisects the angle between the atoms H, O and H (main rotational axis). The positions of the atoms in cartesian coordinates are as follows:
The molecule lies within the plane yz and axis z which bisects the angle between the atoms H, O and H (main rotational axis). The positions of the atoms in cartesian coordinates are as follows:
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
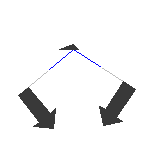
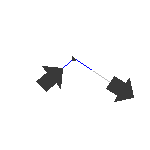
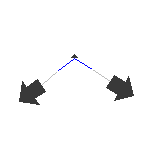
The next three illustrations have the atomic motions introduced into the structure:
| Bending
1960 cm-1 |
Asymmetric stretching
4084 cm-1 |
Symmetric stretching
4049 cm-1 |
|---|---|---|
 |
 |
 |
| VRML file
7589 Bytes
AVI file 109920 Bytes |
VRML file
7545 Bytes
AVI file 109936 Bytes |
VRML file
7552 Bytes
AVI file 109934 Bytes |
For water, the character table for symmetry point group C2v is applied:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We now try to find the irreducible representation to the bending vibration (observed at 1960 cm-1). Identity is without effect to this vibrational mode, this is indicated by a 1 in the respective column.
| E | C2 | σv | σv' |
|---|---|---|---|
| 1 |
As well, rotation around axis C2, i.e. axis z, does not affect the vibrational vectors. Again, we note down 1 in the respective column of the table.
| E | C2 | σv | σ'v |
|---|---|---|---|
| 1 | 1 |
Finally, the motion vectors obtained from reflections on the plane xz and plane yz respectively, are identical to the initial ones. Again, 1 appears in the table.
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
If we compare our findings with the four rows of the character table, it appears that the symmetry properties of the bending vibrational mode match with A1 as irreducible representation.
An analogous investigation for the symmetric streching mode yields A1 too whereas the antisymmetric stretching mode is affected by the symmetry elements C2 and σ. Therefore, this mode corresponds with another irreducible representation and is labelled with Mulliken symbol B2.
| Vibrational mode | Energy / cm-1 | Mulliken Symbol |
|---|---|---|
| Bending |
|
|
| symm. stretching |
|
|
| asymm. stretching |
|
|
Pay attention to the fact that sometimes, another orientation of the molecule is chosen. With the three atoms positioned in plane xz (instead of yz), the symmetry element σv replaces σv' and vice versa. In consequence, the asymmetric stretching is classified as B1 instead of B2.
The vibrations have been calculeted with the MNDO method. For the three vibrational modes and the eigenvalues (respective wave numbers), the components x, y and z of the vibrational eigenvectors are listed in the table.
| Wavenumber | H | O | H | |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.