Vibrational and
Vibrational-Rotational Spectra

Let us consider a typical potential energy curve of a diatomic molecule. In region close to the equilibrium nuclear separation $R_e$ the potential energy can be approximated by a parabola

$$V=\frac{1}{2}k (R-R_e)^2,$$ (55)

where $k$ is a force constant.

The corresponding vibrational energy states are the energies of the harmonic oscillator:

$$E_v = (v+\frac{1}{2})\hbar \omega, \:\:\:\: \omega=\left(\frac{k}{m_{eff}} \right)^{1/2}$$ (56)

with the quantum number $v=0,1,2,\ldots$.

In general, when the approximation in eq. (55) is not valid, the energy levels should be obtained as a solution of the corresponding Schrödinger equation, however, they still can be classified by the quantum number $v$ (for a diatomic molecule case).

If the molecule in its equilibrium position has a dipole moment, as is always the case for the heteroatomic molecules, this dipole moment will in general change if the internuclear distance changed. Thus, on the basic of classical electrodynamics the molecular vibration would lead to the emission of light at the oscillation frequency. Conversely, the oscillator could be set in vibration by absorption of light at this frequency. Therefore, all heteroatomic molecules in principle are said to be infrared active, that is they can absorb or emit infrared radiation. Contrary, all homoatomic diatomic molecules do not have any dipole moment and cannot set in vibration by absorption the infrared light. These molecules are said to be infrared inactive.

The selection rules for the vibrational transitions in a harmonic oscillator-like molecule are

$$\Delta v = v'-v'' = \pm 1$$ (57)

As the energy difference between each two neighbor vibrational energy levels is $\hbar\omega$ (see eq. (56)), the vibrational spectrum would contain only one line which is in fact detected experimentally. This line is called fundamental line. The wavelength of this line for different diatomic molecules usually lies in near IR spectral range $\lambda = 2 \ldots 20\, mkm$.

However, for high lying vibrational energy states the harmonic oscillator approximation in is not valid any more. Usually additional terms proportional to $(R-R_e)^n$, $n=3,4,..$ has to be added to the expression for the potential curve in eq. (55) which leads to the case of the anharmonic oscillator. For anharmonic oscillator the selection rule in eq. (57) is not valid and additional lines appear in the molecular vibration spectra corresponding to transitions with $\Delta v = \pm 2, \pm 3$, and so on. These transitions are called second harmonic, third harmonic, and so on. The intensity of the harmonic transitions transitions is usually much smaller than the intensity of the fundamental line.

In high resolution spectra the vibrational lines in the near IR are resolved into a number of individual lines which are due to vibrational-rotational transitions. A detailed quantum mechanical analysis of simultaneous vibrational and rotational transitions shows that the rotational quantum number $J$ changes by $\pm 1$ during the vibrational transition. If the molecule also possesses angular momentum about its axis, (for instance, $NO(^2\Pi)$), then the selection rule also allows $\Delta J =0$. The appearance of the vibrational-rotational spectrum of a diatomic molecule can be discusses in terms of the combined vibrational-rotational terms

$$S(v,J) = G(v)+F(J) \approx (v+\frac{1}{2})\nu_0 + B J(J+1)$$ (58)

When the vibrational transition $v+1 \leftarrow v$ occurs $J$ changes by $\pm 1$, (or $0, \pm 1$) and the absorption spectrum falls into three groups called branches of the spectrum. The P branch consists of all transitions with $\Delta J = -1$:

$$\omega_P = S(v+1,J-1)- S(v,J) \approx \nu_0 - 2 B J$$ (59)

The Q branch consists of all transitions with $\Delta J =0$:

$$\omega_Q = S(v+1,J-1)- S(v,J) \approx \nu_0$$ (60)

This branch if it is allowed appear at one vibrational transition wavenumber. The R branch consists of all transitions with $\Delta J = 1$:

$$\omega_R = S(v+1,J+1)- S(v,J) \approx \nu_0 + 2 B (J+1)$$ (61)

The intensities of all branches depends both on the population of the vibrational levels and the magnitude of the corresponding $J''\leftarrow J'$ transitions.

The expression for the vibrational-rotational energy term in eq.(58) is given assuming that the rotational and vibrational movements in the molecule are independent from each other and can be treated as zero-order approximation. In fact, this approximation is usually not exact enough in molecular spectroscopy. Particularly, correction of the rotational term by centrifugal interaction is given in eq. (47). More, quantum mechanical analysis shows that the rotational constant $B$ and centrifugal distortion constant $D$ in general also depend on the vibrational quantum number $v$. That is, we have to write $B_v$ and $D_v$ instead of $B$ and $D$. In the first approximation assuming that the rotational-vibrational interaction is small one can write the rotational constant $B_v$ in the form

$$B_v = B_e - \alpha_e\left(v+\frac{1}{2}\right),$$ (62)

where $B_e$ is a "pure" rotational constant given in eq.(36) and the coefficient $\alpha_e$ is assumed to be small compared with $B_e$.

Similarly, the centrifugal distortion constant $D_v$ can be presented as

$$D_v = D_e - \beta_e\left(v+\frac{1}{2}\right),$$ (63)

where $D_e$ is a "pure" centrifugal constant which does not depend on vibration and the coefficient $\beta_e$ is assumed to be small compared with $D_e$.

The examples for $HCl$ are given in Table 2 and Table 3

Table 2: Example $HCl$, $\alpha _e = 0.3072$

State	$e$	$v=1$	$v=2$	$v=3$	$v=4$
B /$cm^{-1}$	10.5934	10.44	10.13	9.83	9.52

Table 3: Example $HCl$, $\beta _e = 7.51\cdot 10^{-6}$

State	e	v=1	v=2	v=3	v=4
B /$cm^{-1}$	$5.32\cdot 10^{-4}$	$5.28\cdot 10^{-4}$	$5.21\cdot 10^{-4}$	$5.13\cdot 10^{-4}$	$5.05\cdot 10^{-4}$

In the first approximation the rotation-vibration energy term is usually presented in the form:

$$S(v,J) = G(v)+F(J)$$

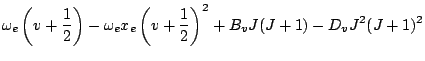$$\approx \omega_e\left(v+\frac{1}{2}\right) - \omega_e x_e\left(v+\frac{1}{2}\right)^2 + B_v J(J+1) - D_v J^2(J+1)^2$$ (64)

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.