



Next: Normal Vibrational Modes
Up: Symmetry of Molecular Vibrations
Previous: Symmetry of Molecular Vibrations
Contents
The classical expression for the vibrational energy, using molecular-fixed 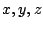 coordinates
(
coordinates
(
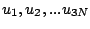 ) = (
) = (
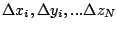 ) is
) is
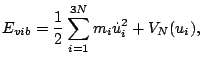 |
|
|
(2) |
where 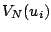 is the potential energy which is zero at the equilibrium together with its
first derivative. The Taylor's series expansion about the equilibrium is
is the potential energy which is zero at the equilibrium together with its
first derivative. The Taylor's series expansion about the equilibrium is
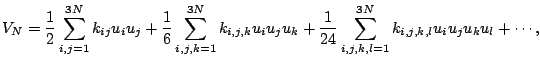 |
|
|
(3) |
where
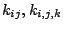 and
and 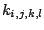 are force constants.
are force constants.
The lowest order terms in the expansion are quadratic and for small displacement only these
terms can be preserved in eq. (3), while all other terms can be neglected.
Corresponding expression for the potential 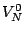 is called the harmonic-oscillator
approximation. In the harmonic-oscillator approximation the vibrational energy can be written
as
is called the harmonic-oscillator
approximation. In the harmonic-oscillator approximation the vibrational energy can be written
as
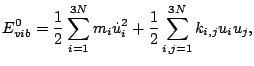 |
|
|
(4) |
where 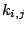 are harmonic force constants.
are harmonic force constants.




Next: Normal Vibrational Modes
Up: Symmetry of Molecular Vibrations
Previous: Symmetry of Molecular Vibrations
Contents
Markus Hiereth
2005-02-09
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
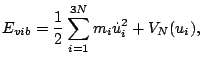
![]() is called the harmonic-oscillator
approximation. In the harmonic-oscillator approximation the vibrational energy can be written
as
is called the harmonic-oscillator
approximation. In the harmonic-oscillator approximation the vibrational energy can be written
as