Spektrales Verteilungsgesetz:
Strahlung eines schwarzen Körpers

Das Maxwellsche Verteilungsgesetz gibt uns die relative Anzahl von Teilchen bei einer Geschwindigkeit v (korrekter: in dem Geschwindigkeitsintervall [v,v+dv] ) an. Wer in kalten Wintertagen an der Heizung steht oder sich eine Wärmflasche auf den Bauch legt, weiss, dass jeder Körper durch Abstrahlung von elektromagnetischer Strahlung Energie verliert. Je höher die Temperatur ist, um so kurzwelliger ist die Strahlung: Ein heißer "Kanonenofen" leuchtet von dunkelrot über hellrot und gelb bis weiß, je höher seine Temperatur ist. Auch wenn der Ofen nicht so extrem heiß ist, spüren wir das abgestrahlte Licht, z.B. eines heißwasserdurchströmten Heizkörpers, in Form von Wärmestrahlung. Die Sonne sendet aufgrund ihrer hohen Temperatur Licht im sichtbaren Spektralbereich aus. Die Gesetze für die spektrale Intensitätsverteilung der Temperaturstrahlung konnte erstmals Max Planck im Jahr 1900 korrekt beschreiben.  Die Energiedichte der Strahlung u(ν)dn (im Frequenzintervall [ν, ν+dν]), also
 

   u(ν)dν  =  Strahlungsenergie im Bereich [ν, ν+dn]/Volumen 
ist gegeben durch:
   u(ν)dν  = 8πhν³/c³/e+hν/kT− 1 dν

Die Grösse h wird nach ihrem Entdecker Planck-Konstante genannt:
 

   h = 6,626176·10-34 Js 
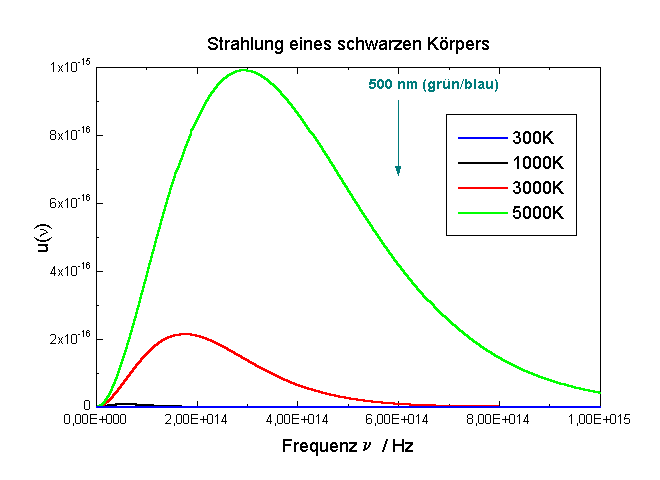Abb. 1: Spektrale Energiedichte als Funktion der Frequenz bei unterschiedlichen Temperaturen.
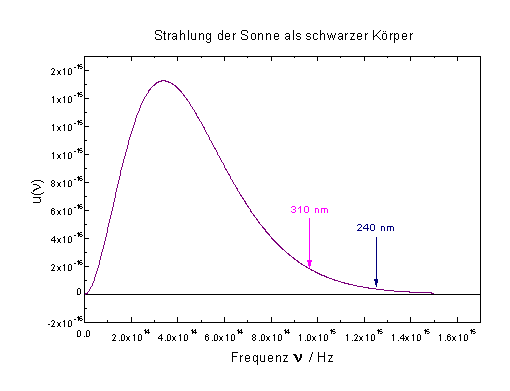Abb. 2: Spektrale Energiedichte der Sonnenstrahung bei der Oberflächentemperatur von ca. T=5770K. Bei dieser Temperatur liegen noch grosse Anteile der Strahlung im blauen bzw. ultravioletten Spektralbereich, was die wesentliche Triebfeder der chemischen Prozesse in unserer Erdatmosphäre ist.

Für das Maximum der Verteilung erhält man (Differenzieren nach ν und Nullsetzen): νmax = 2,8214 kT/h
Daraus lässt sich beispielsweise die Oberflächentemperatur der Sonne zu 5500°C (=5770K) bestimmen.
Die Temperatur des Weltalls beträgt (zurzeit) nur 2,9 K; doch die spektrale Verteilung gehorcht ebenfalls dem Planckschen Strahlungsgesetz, wobei die Frequenzen im Ghz-Bereich liegen (geringe Abweichungen vom Planckschen Gesetz geben Hinweise auf den Ursprung des Weltalls, wie die Galaxienbildung).
 


Integration der Planckschen Gleichung liefert die insgesamt abgestrahlte Energie bei einer Temperatur T und man erhält ist das Strahlungsgesetz von Stefan und Boltzmann:
 
   o∫∞ u(ν)dn  =  U(T)  =  aT4
(a = 7,56·10-16 Jm-3K-4)

Die Intensität (abgestrahlte Energie pro Fläche und Zeit) ist  I = 1/4 c · a · T4
 

I = σoT4[W/m²]
    so ≈  5,6697 · 10-8 [Wm-2K-4] 

Wenden wir das Strahlungsgesetz auf die Sonne an, dann erhalten wir eine abgestrahlte Intensität von ca. I = 6,3·107 W/m² .
Da der Sonnenradius ca. 700000 km beträgt und die Erde ca. 150 Millionen km von der Sonne entfernt ist, kommt von der Intensität nur (700000/150000000)2 zur Erde, d.h. die Intensität der Sonneneinstrahlung  auf die Erde beträgt ca. 1,35  kW/m².
 




Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.