Arrhenius-Gleichung

Die Temperaturabhängigkeit der Reaktionsgeschwindigkeit

Nach dem einfachen Stossmodell findet eine Reaktion dann statt, wenn die beiden Edukte A+B zusammenstossen. Beispiele für eine recht gute Übereinstimmung sind die Reaktionen vom O(1D)-Atom mit H2O, bei der die Geschwindigkeitskonstate k recht gut mit der
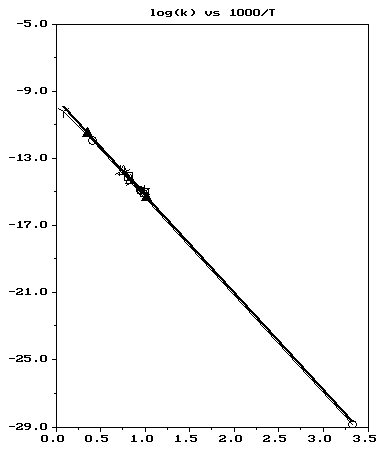Abb.1: Die Temperaturabhängigkeit der Reaktion H+CO2→ OH+CO. Ergibt die Auftragung von  ln k gegen 1/T eine Gerade, dann wird k(T) durch die Arrhenius-Gleichung beschrieben.
Stossfrequenz, die sich aus der kinetischen Stosstheorie ergibt, übereinstimmt: k = ZAB. Im Allgemeinen führt jedoch nicht jeder Stoss auch zu einer chemischen Reaktion, vielmehr ist das Überwinden einer energetischen Barriere notwendig, und nur die Moleküle haben eine Chance zu reagieren, die zumindest genügend Energie besitzen (die Aktivierungsenergie Ea), um diese Barriere zu überwinden. Von der Boltzmannverteilung für die kinetische Energie, G(E)dE, wissen wir bereits, dass dieser Bruchteil f der Moleküle mit ausreichend Energie (E>Ea) im wesentlichen propotional zu e-Ea/RT ist, d.h. wir erhalten für die Geschwindigkeitskonstante k = ZAB. f :

k = ZAB . e-Ea/RT
Hinsichtlich der Temperaturänderung ändert sich die Stossfrequenz ZAB nur wenig mit der Temperatur (~T1/2: Temperaturerhöhung von 200°C nach 300°C ändert ZAB um weniger als 10%). Es ist daher eine recht gute Annäherung, ZAB als konstant anzusetzen und wir erhalten die Arrhenius-Gleichung (Arrhenius fand diese Gleichung empirisch in umfangreichen Studien):
 
k  =  A e−Ea/RT

Man kann diese Gleichung auch in der Form

ln k  =  ln A − Ea/RT

schreiben. Danach erhält man eine Gerade, wenn man ln k gegen 1/T aufträgt. A nennt man den präexponentiellen Faktor oder auch Frequenzfaktor, Ea die Aktivierungsenergie. In der Tabelle sind einige experimentelle Werte zusammengestellt:
 

Arrhenius-Parameter
(1) Reaktionen 
erster Ordnung		 A / s-1 Ea / kJ mol-1
N2O5 → NO2 + NO3
CH3NC → CH3CN 
2 N2O5 → 4 NO2 + O2		 1,2 · 1015
3,8 · 1013
6,31 · 1014		 92,8 
161 
88
(2) Reaktionen 
zweiter Ordnung		 A Ea / kJ mol-1
O + H2  → OH + H
OH + H2 → H2O + H 
H + CO2 → OH + CO
C2H5ONa + CH3I   in Ethanol 		 7,1· 10-11 Molek-1s-1
3,5· 10-10 Molek-1s-1
8,0 · 1010mol-1s-1
2,4 · 1011 mol-1s-1		 109,6 
41,1 
42,0 
81,6 

 
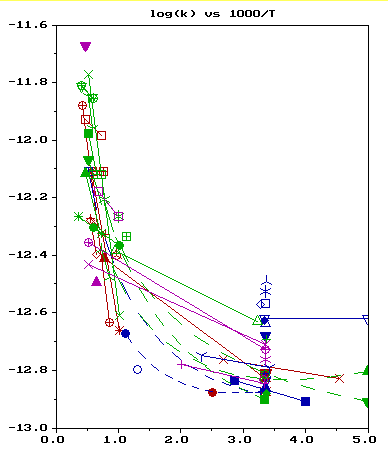Abb.2.: Die Temperaturabhängigkeit der Reaktion OH+CO ® H+CO kann nicht durch die Arrheniussche Gleichung beschrieben werden, da eine Auftragung aller gemessenen k(T)- Werte in der Form ln k(T) gegen 1/T keine Gerade ergibt.

In manchen Fällen gehorcht die Temperaturabhängigkeit nicht der Formel von Arrhenius. Ein Beispiel hierfür ist die Reaktion OH+CO → H+CO, deren Geschwindigkeitskonstante - aufgrund der atmosphärischen Bedeutung - sehr häufig gemessen wurde (Abb.2). Gründe hierfür sind die Nichtberücksichtigung der inneren Energien der Edukte (die Stosstheorie berücksichtigt nur die kinetische Energie des Stosses) und der sogenannte Sterische Faktor S, der berücksichtigt, dass Moleküle nur dann reagieren könne, wenn die räumlich Anordnung dies zulässt. Im einfachen Beispiel der Reaktion  Br + HI → HBr + I ist klar, dass HBr nur dann entstehen kann, wenn das Br auf das H-Atom im HI-Molekül stösst und nicht auf das I-Atom. Einige kleine Filmchen zur Illustration des Sterischen Faktors gibt's hier. Die leicht modifizierte Arrheniussche Gleichung lautet danach:
 

k  =  S·A e−Ea/RT

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.