Aus der Reaktionsgleichung, die die Photodissoziation von Ozon bei der Frequenz ν (Wellenlänge λ) beschreibt,
O3 + hν (l £ 310 nm) → O + O2
können wir das Geschwindigkeitsgesetz für den Abbau von Ozon aufstellen:
d[O3]/dt = − k [hν] [O3]
dabei kennzeichnet das Minuszeichen den Abbau von O3 und die eckige Klammer [O3] steht für die Konzentration von Ozon, d.h. Zahl der O3-Moleküle pro cm3. Für [hν] bedeutet dies: Zahl der Photonen bei der Frequenz ν pro cm3. Nun kennen wir schon aus den ersten Überlegungen zur Reaktionsdynamik, dass k = σ·v ist. Bei Licht ist v = c, also die Lichtgeschwindigkeit, und σ ist der Absorptionsquerschnitt bei der Frequenz ν (resp. Wellenlänge λ = c/ν). Ist die Quantenausbeute φ für den Zerfallskanal ungleich eins, dann fügt man φ noch mit ein: k = σ·c·φ. Man kommt so zu der Grösse c[hν], die, wenn wir c in cm/s angeben, die Dimension [cm/s·Photonen/cm³ = Photonen/(cm²s) ] hat, was nichts anderes als die bereits eingeführte Intensität I (korrekt der Photonenfluss) ist. Wir erhalten also
d[O3]/dt = − I · s · f [O3]
Diese Differentialgleichung können wir sofort lösen, wenn
wir annehmen, dass sich die Intensität nicht mit der Zeit ändert,
denn dann handelt es sich um eine einfache Reaktion
1. Ordnung. Vorher aber noch einige Worte zu den Größen
I, σ und φ, die alle
von der Frequenz (bzw. Wellenlänge) abhängen. Die Intensität
des Sonnenlichts in der Atmosphäre ist natürlich stark von der
Wellenlänge λ vom Einfallswinkel und der
Absorption durch Moleküle in größeren Höhen abhängig.
Um nun die Gesamtwirkung bei allen Wellenlängen zu erhalten, müssen
wir über die Wellenlänge integrieren:
| J = ò Ils(λ) φ(λ) dλ |
wobei Iλ die Intensität im
Wellenlängenintervall [λ,λ+dλ]
angibt. Diese Größe Iλ
nennt man für unsere Erdatmosphäre auch aktinischer Fluss.
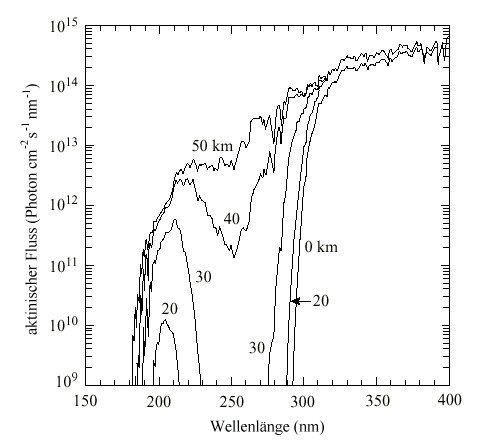 |
| Abb. 1: Der aktinische Fluss für unterschiedliche Höhen (in km) als Funktion der Wellenlänge |
In der Abbildung 1 ist der aktinische Fluss der Sonne als Funktion der
Wellenlänge für unterschiedliche Höhen dargestellt.
Da um 550 nm die Zahl der Photonen pro Sekunde durch P/hν
= P · λ/hc
gegeben ist, erhalten wir:
d[O3]/dt = − J·[O3]
Die Dimension von J ist s−1, was der Dimension einer Geschwindigkeitskonstanten 1. Ordnung entspricht.
Die Integration ist nun leicht auszuführen, wenn wir annehmen, dass zum Zeitpunkt t = 0 die Ozonkonzentration [O3]o sein und J nicht von der Zeit abhängt. Dies letztere stimmt in der Atmosphäre natürlich nicht ganz, da bekanntlich die Sonne aufgeht und auch Wolken das Sonnenlicht stärker beeinflussen. Aber wir gehen der einfachheithalber von einem konstanten mittleren J aus und erhalten:
ln [O3]/[O3]o = − J t
| [O3] = [O3]o e−J t |
Der Wert von J hängt stark von der Höhe und der Jahres/Tageszeit ab. In der Stratosphäre ist J ca. 4·10-3s-1, d.h. innerhalb weniger Minuten ist das Ozon komplett photolysiert, also vollständig abgebaut, was glücklicherweise nicht in der Wirklichkeit geschieht. Was haben wir danach falsch gemacht? Nichts, doch wir haben etwas vergessen und das wollen wir im nächsten Kapitel berücksichtigen.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.