


Next: Entkopplung der Elektronenbewegung
Up: Die Born-Oppenheimer-Näherung
Previous: Die Born-Oppenheimer-Näherung
In der Chemie benutzt man anschauliche Modelle um die Struktur von
Molekülen und deren verschiedenartige Reaktionen (Dynamik) zu beschreiben
und zu verstehen.
Durch die Quantenmechanik hat man einen strengen theoretischen Zugang
zur Struktur und Dynamik von Molekülen: das Verhalten eines chemischen
Systems ergibt sich aus der Schrödinger-Gleichung für dessen Bestandteile:
Elektronen und Atomkerne
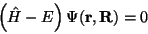 |
(1) |
Die sog. Wellenfunktion, 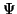 ,
hängt von den Koordinaten der
Elektronen,
r, und der Atomkerne,
R, ab
(Wir werden vektorielle Größen entweder fett schreiben oder mit
einem Pfeil kennzeichnen).
,
hängt von den Koordinaten der
Elektronen,
r, und der Atomkerne,
R, ab
(Wir werden vektorielle Größen entweder fett schreiben oder mit
einem Pfeil kennzeichnen).
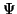 selbst hat keine direkte physikalische Bedeutung, die entscheidende
Größe ist das Quadrat ihres Betrages,
selbst hat keine direkte physikalische Bedeutung, die entscheidende
Größe ist das Quadrat ihres Betrages, 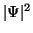 ,
die
Aufenthaltswahrscheinlichkeitsdichte für die Elektronen und
Atomkerne.
Zu jedem
,
die
Aufenthaltswahrscheinlichkeitsdichte für die Elektronen und
Atomkerne.
Zu jedem 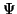 ,
das Lösung von Gln. (1) ist, gehört ein bestimmter
Energieeigenwert E. I.a. gibt es unendlich viele Lösungen
(d.h. Zustände des chemischen Systems),
von denen insbesondere derjenige mit der tiefsten Energie (der Grundzustand)
von Interesse ist.
,
das Lösung von Gln. (1) ist, gehört ein bestimmter
Energieeigenwert E. I.a. gibt es unendlich viele Lösungen
(d.h. Zustände des chemischen Systems),
von denen insbesondere derjenige mit der tiefsten Energie (der Grundzustand)
von Interesse ist.
Der Hamilton-Operator, 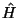 ,
läßt sich im einfachsten Fall
(d.h. keine Zeitabhängigkeit, nicht-relativistische Näherung,
kein äußeres Feld), sofort angeben:
,
läßt sich im einfachsten Fall
(d.h. keine Zeitabhängigkeit, nicht-relativistische Näherung,
kein äußeres Feld), sofort angeben:
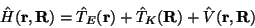 |
(2) |
Er besteht aus den Operatoren für die kinetische Energie der
Elektronen, 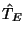 ,
und der Atomkerne,
,
und der Atomkerne, 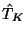 ,
,
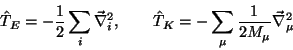 |
(3) |
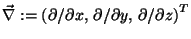 ist der Operator für den Gradienten
und M ist die Masse eines Atomkerns.
Es werden hier, wie auch im übrigen Teil der Vorlesung, ausschließlich
atomare Einheiten verwendet, d.h. wir setzen
ist der Operator für den Gradienten
und M ist die Masse eines Atomkerns.
Es werden hier, wie auch im übrigen Teil der Vorlesung, ausschließlich
atomare Einheiten verwendet, d.h. wir setzen
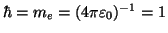 .
.
Der Operator für die potentielle Energie ist gegeben durch
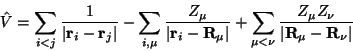 |
(4) |
Z ist die elektrische Ladung eines Atomkerns.
Wir verwenden für Elektronen die Indizes i und j und für Atomkerne
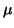 und
und 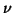 .
r und
R sind, wie schon erwähnt, die Koordinatenvektoren eines
Elektrons, bzw. eines Atomkerns.
Sind bei ersteren keine Indizes angegeben, wie z.B. in Gln. (1),
so stehen sie für die Gesamtheit aller Elektronen-, bzw. Kern-Koordinaten.
.
r und
R sind, wie schon erwähnt, die Koordinatenvektoren eines
Elektrons, bzw. eines Atomkerns.
Sind bei ersteren keine Indizes angegeben, wie z.B. in Gln. (1),
so stehen sie für die Gesamtheit aller Elektronen-, bzw. Kern-Koordinaten.
Neben der Schrödinger-Gleichung (1) muß die Wellenfunktion
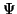 eines chemischen Systems noch weiteren Nebenbedingung genügen,
um den Elektronenspin und das Pauli-Prinzip zu berücksichtigen.
Diese Nebenbedingungen bestehen aus besonderen Symmetriebedingung bezüglich
des Vertauschens von zwei Elektronen, bzw. von zwei gleichartigen
Atomkernen und werden erst in späteren Vorlesungsstunden behandelt.
In dieser ersten Vorlesungsstunde gehen wir davon aus, daß diese
Nebenbedingungen erfüllt sind, ohne daß wir sie ausdrücklich
angeben.
Deren genaue Form benötigen wir erst später.
eines chemischen Systems noch weiteren Nebenbedingung genügen,
um den Elektronenspin und das Pauli-Prinzip zu berücksichtigen.
Diese Nebenbedingungen bestehen aus besonderen Symmetriebedingung bezüglich
des Vertauschens von zwei Elektronen, bzw. von zwei gleichartigen
Atomkernen und werden erst in späteren Vorlesungsstunden behandelt.
In dieser ersten Vorlesungsstunde gehen wir davon aus, daß diese
Nebenbedingungen erfüllt sind, ohne daß wir sie ausdrücklich
angeben.
Deren genaue Form benötigen wir erst später.



Next: Entkopplung der Elektronenbewegung
Up: Die Born-Oppenheimer-Näherung
Previous: Die Born-Oppenheimer-Näherung
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() ,
läßt sich im einfachsten Fall
(d.h. keine Zeitabhängigkeit, nicht-relativistische Näherung,
kein äußeres Feld), sofort angeben:
,
läßt sich im einfachsten Fall
(d.h. keine Zeitabhängigkeit, nicht-relativistische Näherung,
kein äußeres Feld), sofort angeben:
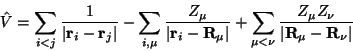
![]() eines chemischen Systems noch weiteren Nebenbedingung genügen,
um den Elektronenspin und das Pauli-Prinzip zu berücksichtigen.
Diese Nebenbedingungen bestehen aus besonderen Symmetriebedingung bezüglich
des Vertauschens von zwei Elektronen, bzw. von zwei gleichartigen
Atomkernen und werden erst in späteren Vorlesungsstunden behandelt.
In dieser ersten Vorlesungsstunde gehen wir davon aus, daß diese
Nebenbedingungen erfüllt sind, ohne daß wir sie ausdrücklich
angeben.
Deren genaue Form benötigen wir erst später.
eines chemischen Systems noch weiteren Nebenbedingung genügen,
um den Elektronenspin und das Pauli-Prinzip zu berücksichtigen.
Diese Nebenbedingungen bestehen aus besonderen Symmetriebedingung bezüglich
des Vertauschens von zwei Elektronen, bzw. von zwei gleichartigen
Atomkernen und werden erst in späteren Vorlesungsstunden behandelt.
In dieser ersten Vorlesungsstunde gehen wir davon aus, daß diese
Nebenbedingungen erfüllt sind, ohne daß wir sie ausdrücklich
angeben.
Deren genaue Form benötigen wir erst später.