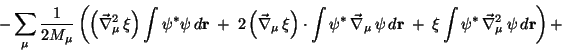Next: Die Schrödinger-Gleichung der Kernbewegung
Up: Die Born-Oppenheimer-Näherung
Previous: Die Schrödinger-Gleichung
In 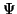 ,
der Lösung der Schrödinger-Gleichung (1), werden Elektronen
und Atomkerne formal gleichbehandelt.
Diese Tatsache wiederspricht dem üblichen ``chemischen'' Modell des Aufbaus
eines Moleküls aus einzelnen, zueinander gebundenen ``Atomen.''
Da ein Atomkern mindestens 2000-mal schwerer ist als ein Elektron,
könnte man annehmen, daß die Elektronen der Bewegung der Atomkerne nahezu
unmittelbar folgen können und daß sich letztere schließlich in dem
elektrostatischen Feld bewegen, welches aus den übrigen Atomkernen und allen
Elektronen gebildet wird.
,
der Lösung der Schrödinger-Gleichung (1), werden Elektronen
und Atomkerne formal gleichbehandelt.
Diese Tatsache wiederspricht dem üblichen ``chemischen'' Modell des Aufbaus
eines Moleküls aus einzelnen, zueinander gebundenen ``Atomen.''
Da ein Atomkern mindestens 2000-mal schwerer ist als ein Elektron,
könnte man annehmen, daß die Elektronen der Bewegung der Atomkerne nahezu
unmittelbar folgen können und daß sich letztere schließlich in dem
elektrostatischen Feld bewegen, welches aus den übrigen Atomkernen und allen
Elektronen gebildet wird.
Um dieser Vorstellung vom Aufbau eines Moleküls gerecht zu werden, schreiben
wir die Wellenfunktion 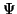 als das Produkt einer Funktion
als das Produkt einer Funktion 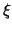 ,
die nur von
den Koordinaten der Atomkerne abhängt, mit einer Funktion
,
die nur von
den Koordinaten der Atomkerne abhängt, mit einer Funktion 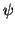 ,
die sowohl
von den Elektronenkoordinaten, als auch von den Kernkoordinaten abhängt
(vergl. Ref. [1,2])
,
die sowohl
von den Elektronenkoordinaten, als auch von den Kernkoordinaten abhängt
(vergl. Ref. [1,2])
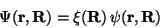 |
(5) |
Eine ähnliche Zerlegung nehmen wir für den Hamilton-Operator (2) vor
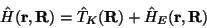 |
(6) |
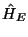 ist der sog. ``elektronische Hamilton-Operator''
ist der sog. ``elektronische Hamilton-Operator''
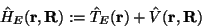 |
(7) |
Die Kern-Kern-Wechselwirkung,
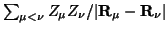 ,
wird ebenfalls in
,
wird ebenfalls in 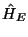 untergebracht;
man nennt
untergebracht;
man nennt 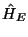 auch den Hamilton-Operator der
festgehefteten Atomkerne, engl.: clamped-nuclei hamiltonian.
auch den Hamilton-Operator der
festgehefteten Atomkerne, engl.: clamped-nuclei hamiltonian.
Wir wollen nun die Konsequenz der Zerlegungen (5) und (6)
untersuchen, und setzen sie zu diesem Zweck in die Schrödinger-Gleichung
(1) ein
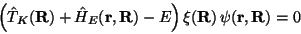 |
(8) |
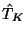 wirkt auf beide Anteile der Wellenfunktion, siehe Gln. (5),
während
wirkt auf beide Anteile der Wellenfunktion, siehe Gln. (5),
während 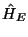 nur
nur 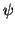 verändert.
Gln. (8) wird also unter Berücksichtigung der Gestalt von
verändert.
Gln. (8) wird also unter Berücksichtigung der Gestalt von
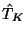 ,
siehe Gln. (3), zu
,
siehe Gln. (3), zu
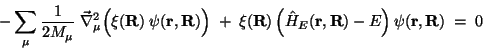 |
(9) |
Das Differenzieren der Gesamtwellenfunktion nach den Kernkoordinaten, wie es
im ersten Summanden auftritt, ergibt
Wir setzen nun das Ergebnis dieser Nebenrechnung in Gln. (9) ein,
multiplizieren von links mit 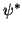 und integrieren über die
Elektronenkoordinaten
r; der Übersichtlichkeit halber lassen
wir die Argumente der Funktionen weg
und integrieren über die
Elektronenkoordinaten
r; der Übersichtlichkeit halber lassen
wir die Argumente der Funktionen weg
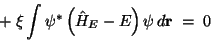 |
(11) |
Wir nehmen nun an, daß 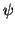 bezüglich der Elektronenkoordinaten
r auf eins normiert ist, was voraussetzt, daß die Elektronen gebunden
sind
bezüglich der Elektronenkoordinaten
r auf eins normiert ist, was voraussetzt, daß die Elektronen gebunden
sind
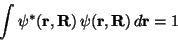 |
(12) |
In diesem Fall läßt sich die Funktion 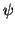 reell wählen und wir erkennen,
daß der rechte Teil des zweiten Summanden in Gln. (11) als Gradient des
konstanten Normierungsintegrals (12) verschwindet
reell wählen und wir erkennen,
daß der rechte Teil des zweiten Summanden in Gln. (11) als Gradient des
konstanten Normierungsintegrals (12) verschwindet
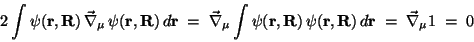 |
(13) |
Gln. (11) vereinfacht sich also zu
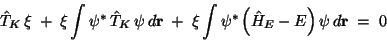 |
(14) |
Wir definieren nun die Größen
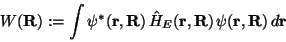 |
(15) |
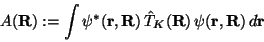 |
(16) |
und
|
W'(R) := W(R) + A(R)
|
(17) |
und erhalten schließlich die gewünschte Schrödinger-Gleichung für die
Bewegung der Atomkerne
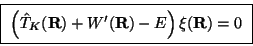 |
(18) |



Next: Die Schrödinger-Gleichung der Kernbewegung
Up: Die Born-Oppenheimer-Näherung
Previous: Die Schrödinger-Gleichung
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() als das Produkt einer Funktion
als das Produkt einer Funktion ![]() ,
die nur von
den Koordinaten der Atomkerne abhängt, mit einer Funktion
,
die nur von
den Koordinaten der Atomkerne abhängt, mit einer Funktion ![]() ,
die sowohl
von den Elektronenkoordinaten, als auch von den Kernkoordinaten abhängt
(vergl. Ref. [1,2])
,
die sowohl
von den Elektronenkoordinaten, als auch von den Kernkoordinaten abhängt
(vergl. Ref. [1,2])