Die Schrödinger-Gleichung der Kernbewegung

Die Funktion W'(R) in Gln. (18) nennt man ``Potentialhyperfläche,'' oder bei zweiatomigen Molekülen ``Potentialkurve.'' Die ``adiabatische Korrektur'' A(R) ist im Grunde genommen relativ leicht zu berechnen [3], man verzichtet in der Praxis jedoch meistens darauf (d.h. man setzt 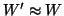$W'\approx W$) da A(R) so klein ist, daß die übrigen Fehler meist viel größer sind. 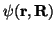Um eine Vorstellung von der Größe von A(R) zu bekommen, kann man sich überlegen, daß die zweite Ableitung der elektronischen Wellenfunktion $\psi(\mathbf{r},\mathbf{R})$ nach einer Kernkoordinate im wesentlichen gleich der zweiten Ableitung nach einer Elektronenkoordinate ist, welche schließlich mit dem Kehrwert der Kernmasse gewichtet wird.

  

Abbildung 1:

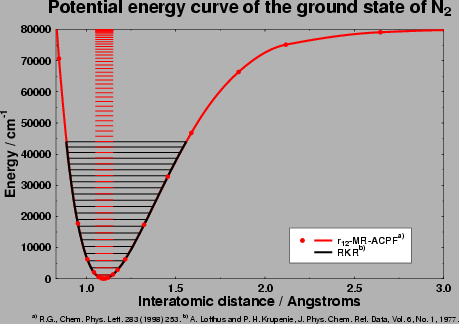Die Abbildung 1 zeigt als Beispiel die Potentialkurve des (elektronischen) Grundzustands des Stickstoff-Dimeren (N₂) [4]. Man sieht, daß in der Nähe des Gleichgewichtsabstandes ( R_e=1.09768₅Å [5]) W(R) ungefähr quadratisch ist. Zu kleineren Abständen steigt die Potentialkurve schnell an, während sie zu größeren Abständen hin zum Dissoziationslimit ( 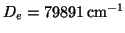$D_e=79891\,{\rm cm}^{-1}$[5]) strebt.

  

Abbildung: Rotierendes zweiatomiges Molekül (schematisch)

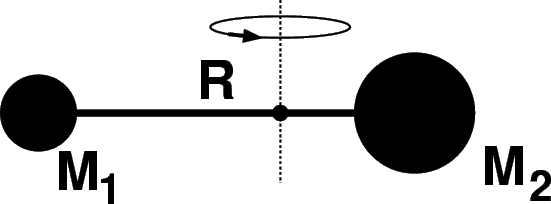Im Fall eines zweiatomigen Moleküls (siehe Abbildung 2) schreibt man üblicherweise die Kern-Schrödinger-Gleichung (18) in der Form

$$\left[ {1\over 2\mu} \left( -{d^2\over d R^2} \;+\; {J(J+1)\over R^2} \right) \;+\; W'(R) \;-\; E \right] \xi(R) \;=\; 0$$ (19)

Hier ist R der Abstand der beiden Atomkerne zueinander, 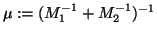$\mu:=(M_1^{-1}+M_2^{-1})^{-1}$ ist die reduzierte Masse und 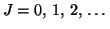$J=0,\,1,\,2,\,\ldots\,$ ist die Rotationsquantenzahl. Im Fall des Grundzustands von N₂ gibt es ca. 60 Vibrationszustände.

Die ro-vibronischen Energieterme eines zweiatomigen Moleküls lassen sich schreiben als

 

$$\omega_e\left(v+{\textstyle{1\over 2}}\right) - \omega_e x_e \left(v+{\textstyle{1\over 2}}\right)^2 + \ldots$$ E(v,J) =

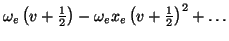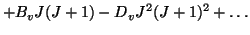$$+ B_v J(J+1) - D_v J^2(J+1)^2 + \ldots$$ (20)

mit den Rotationskonstanten

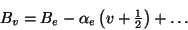$$B_v = B_e - \alpha_e\left(v+{\textstyle{1\over 2}}\right) + \ldots$$ (21)

und den Anharmonizitätskonstanten

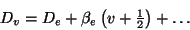$$D_v = D_e + \beta_e\left(v+{\textstyle{1\over 2}}\right) + \ldots$$ (22)

Die Gln. (20) läßt sich auch formal in Form der Dunham-Reihe schreiben

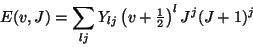$$E(v,J) = \sum_{lj} Y_{lj} \left(v+{\textstyle{1\over 2}}\right)^l J^j (J+1)^j$$ (23)

wobei die Y_lj mit den entsprechenden Molekülkonstanten zu identifizieren sind.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.