


Next: Brechen chemischer Bindungen
Up: Anhang
Previous: Die Slater-Condon-Regeln (für Fortgeschrittene)
Symmetrie
Einen Operator 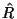 der mit dem Hamiltonoperator
der mit dem Hamiltonoperator 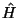 des jeweiligen Systems vertauscht, d.h.
des jeweiligen Systems vertauscht, d.h.
![\begin{displaymath}[\hat R, \hat H]:= \hat R \hat H - \hat H \hat R = 0
\end{displaymath}](img285.gif) |
(129) |
nennt man Symmetrieoperator.
Wichtige Symmetrieoperatoren sind Drehungen (Cn), Spiegelungen (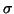 ),
die Inversion (i) und die Drehimpulsoperatoren (L2, Lz) für
räumlichen und Spin-Drehimpuls.
Da der (nicht-relativistische) Hamilton-Operator
),
die Inversion (i) und die Drehimpulsoperatoren (L2, Lz) für
räumlichen und Spin-Drehimpuls.
Da der (nicht-relativistische) Hamilton-Operator 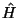 den Spin nicht
enthält, vertauscht er stets mit den Spin-Operatoren
den Spin nicht
enthält, vertauscht er stets mit den Spin-Operatoren 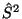 und
und
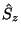 .
.
Wir wollen nun zeigen, daß ein Matrixelement
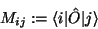 |
(130) |
stets verschwindet, wenn 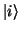 und
und 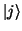 Eigenfunktionen
eines beliebigen hermiteschen Operators
Eigenfunktionen
eines beliebigen hermiteschen Operators 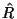 sind, der mit
sind, der mit 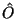 kommutiert und die beiden Eigenwerte
kommutiert und die beiden Eigenwerte 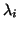 ,
,
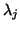 verschieden sind.
Beweis:
verschieden sind.
Beweis:
Gilt nun
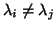 dann folgt zwangsläufig Mij=0,
was zu beweisen war
dann folgt zwangsläufig Mij=0,
was zu beweisen war

Für den Hamilton-Operator folgt damit, daß bei Vorhandensein von Symmetrie,
seine Matrixdarstellung blockdiagonal ist.
Durch die Ausnutzung dieser Eigenschaft läßt sich zum einen (zum Teil
erheblich) Rechenzeit
sparen, zum anderen wird die Dimensionalität des Problems reduziert und
damit die Stabilität des verwendeten Algorithmus erhöht.



Next: Brechen chemischer Bindungen
Up: Anhang
Previous: Die Slater-Condon-Regeln (für Fortgeschrittene)
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.