


Next: Symmetrie
Up: Anhang
Previous: Beweis des Variationstheorems
Die Slater-Condon-Regeln
(für Fortgeschrittene)
Gegeben sind zwei Slater-Determinanten 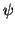 und
und 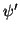 ,
bestehend
aus Orbitalen
,
bestehend
aus Orbitalen 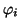 ,
die einer orthonormalen Basis entnommen sind.
Ermittelt werden sollen die Überlappungsmatrixelemente und die
Matrixelemente eines Ein-
,
die einer orthonormalen Basis entnommen sind.
Ermittelt werden sollen die Überlappungsmatrixelemente und die
Matrixelemente eines Ein-
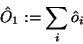 |
(123) |
und eines Zweielektronen-Operators
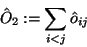 |
(124) |
Sei 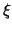 ein nicht-antisymmetrisiertes Orbitalprodukt, so daß
ein nicht-antisymmetrisiertes Orbitalprodukt, so daß
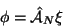 |
(125) |
Mit
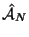 definiert nach Gln. (42)
definiert nach Gln. (42)
wobei
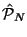 ein N-Teilchenpermutations-Operator ist, T(p) ist die Anzahl
der Transpositionen (paarweise Vertauschungen) der Permutation und es wird
über alle N! mögliche Permutationen summiert.
Es wird weiter angenommen, daß bei den Matrixelementen zweier verschiedener
Determinanten
ein N-Teilchenpermutations-Operator ist, T(p) ist die Anzahl
der Transpositionen (paarweise Vertauschungen) der Permutation und es wird
über alle N! mögliche Permutationen summiert.
Es wird weiter angenommen, daß bei den Matrixelementen zweier verschiedener
Determinanten 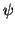 und
und 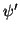 ,
die entsprechenden Orbitalprodukte
,
die entsprechenden Orbitalprodukte
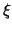 und
und 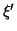 auf die größtmögliche Übereinstimmung gebracht worden
sind.
Gemäß Gln. (42) ist dazu bei einer Vertauschung zweier Orbitale,
das Vorzeichen umzukehren.
auf die größtmögliche Übereinstimmung gebracht worden
sind.
Gemäß Gln. (42) ist dazu bei einer Vertauschung zweier Orbitale,
das Vorzeichen umzukehren.
Überlappungs-Matrixelemente:
Einelektronen-Matrixelemente:
Zweielektronen-Matrixelemente:
![\begin{displaymath}= \left\{
\begin{array}{l}
\sum_{i<j} \big( \langle\varphi_i ...
...en verschieden}\\ [1ex]
0, \mbox{\ sonst}
\end{array} \right.
\end{displaymath}](img283.gif) |
(128) |



Next: Symmetrie
Up: Anhang
Previous: Beweis des Variationstheorems
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
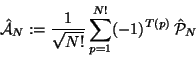
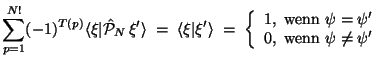
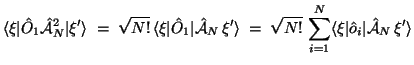
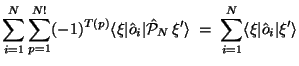
![$\displaystyle \left\{
\begin{array}{l}
\sum_i \langle\varphi_i\vert\hat o_1\ver...
...an einer Stelle verschieden}\\ [1ex]
0, \mbox{\ sonst} \\
\end{array} \right.$](img278.gif)
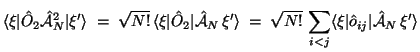
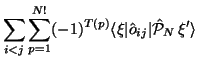
![\begin{displaymath}= \left\{
\begin{array}{l}
\sum_{i<j} \big( \langle\varphi_i ...
...en verschieden}\\ [1ex]
0, \mbox{\ sonst}
\end{array} \right.
\end{displaymath}](img283.gif)