


Next: Der Energie-Erwartungswert
Up: Der Hartree-Fock-Ansatz
Previous: Der Hartree-Fock-Ansatz
Der einfachste Näherungsansatz für die Lösung der Schrödinger-Gleichung
eines Moleküls mit N Elektronen ist ein anti-symmetrisiertes Produkt
bestehend aus N ortho-normalen
Einelektronenfunktionen, den Orbitalen 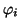
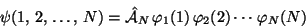 |
(40) |
Wir schreiben hier die Ordnungszahl des jeweiligen Elektrons als
Funktionsargument, also z.B.
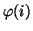 anstelle von
anstelle von
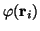 .
Der Antisymmetrisierungsoperator
.
Der Antisymmetrisierungsoperator
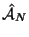 sorgt dafür, daß das Pauli-Prinzip
erfüllt ist, d.h. daß die Wellenfunktion
sorgt dafür, daß das Pauli-Prinzip
erfüllt ist, d.h. daß die Wellenfunktion 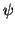 bei einer Vertauschung von
zwei Elektronen ihr Vorzeichen verändert
bei einer Vertauschung von
zwei Elektronen ihr Vorzeichen verändert
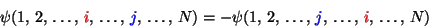 |
(41) |
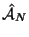 kann explizit geschrieben werden als
kann explizit geschrieben werden als
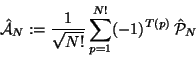 |
(42) |
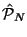 ist ein Operator der N Objekte permutiert, die Summe läuft
über alle möglichen Permutationen und T(p) ist die Anzahl von
Transpositionen, d.h. die kleinste Anzahl von Vertauschungen von Paaren
die notwendig ist, um eine bestimmte Permutation zu erzeugen.
Demnach ist
(-1)T(p) das Vorzeichen der Permutation, also positiv bei
einer geraden Anzahl von Vertauschungen und negativ bei einer
ungeraden Anzahl.
ist ein Operator der N Objekte permutiert, die Summe läuft
über alle möglichen Permutationen und T(p) ist die Anzahl von
Transpositionen, d.h. die kleinste Anzahl von Vertauschungen von Paaren
die notwendig ist, um eine bestimmte Permutation zu erzeugen.
Demnach ist
(-1)T(p) das Vorzeichen der Permutation, also positiv bei
einer geraden Anzahl von Vertauschungen und negativ bei einer
ungeraden Anzahl.
Nach Slater kann man den Hartree-Fock-Ansatz auch in Form einer
Determinanten schreiben (vgl. Lehrbücher der Linearen Algebra,
z.B. Ref. [11])
Der Vorfaktor
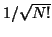 dient der Normierung der Wellenfunktion auf Eins
(siehe Anhang:
Slater-Condon-Regeln).
dient der Normierung der Wellenfunktion auf Eins
(siehe Anhang:
Slater-Condon-Regeln).



Next: Der Energie-Erwartungswert
Up: Der Hartree-Fock-Ansatz
Previous: Der Hartree-Fock-Ansatz
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.