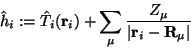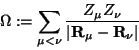Next: Die Hartree-Fock-Gleichungen
Up: Der Hartree-Fock-Ansatz
Previous: Die Slater-Determinante
Wir bestimmen nun den Energie-Erwartungswert indem wir die Slater-Determinante, Gln. (43),
in den Rayleigh-Quotienten, Gln. (27) einsetzen
![\begin{displaymath}
E\big[\varphi_1,\,\varphi_2,\,\ldots,\,\varphi_N\big] =
{\bi...
...vert\varphi_1\,\varphi_2\,\ldots\,\varphi_N\vert\,\big\rangle}
\end{displaymath}](img97.gif) |
(44) |
Zur weiteren Vereinfachung dieses Ausdrucks ist es sinnvoll,
den Hamilton-Operator 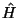 in die folgende Summe aufzuteilen
in die folgende Summe aufzuteilen
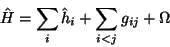 |
(45) |
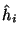 wirkt nur auf das i-te Elektron
wirkt nur auf das i-te Elektron
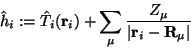 |
(46) |
gij wirkt nur auf das Elektronenpaar i und j
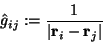 |
(47) |
und 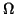 schließlich hängt nur von der Anordnung der Atomkerne ab,
es ist also im elektronischen Hamilton-Operator (7), bzw. (45)
eine Konstante
schließlich hängt nur von der Anordnung der Atomkerne ab,
es ist also im elektronischen Hamilton-Operator (7), bzw. (45)
eine Konstante
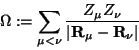 |
(48) |
vergl. den Abschnitt
``Born-Oppenheimer-Näherung.''
Der Energie-Erwartungswert, Gln. (44), läßt sich nun mit Hilfe
der bereits erwähnten
``Slater-Condon-Regeln''
vereinfachen zu
![$\displaystyle {
E\big[\varphi_1,\,\varphi_2,\,\ldots,\,\varphi_N\big] =
\sum_{\red i}\langle\varphi_{\red i}\vert\hat h\vert\varphi_{\red i}\rangle \;+}$](img104.gif) |
| |
|
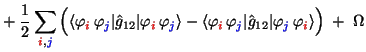 |
(49) |
mit den Ein-
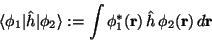 |
(50) |
und Zweielektronen-Integralen
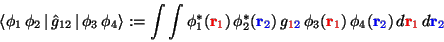 |
(51) |



Next: Die Hartree-Fock-Gleichungen
Up: Der Hartree-Fock-Ansatz
Previous: Die Slater-Determinante
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![\begin{displaymath}
E\big[\varphi_1,\,\varphi_2,\,\ldots,\,\varphi_N\big] =
{\bi...
...vert\varphi_1\,\varphi_2\,\ldots\,\varphi_N\vert\,\big\rangle}
\end{displaymath}](img97.gif)