


Next: Ergänzung
Up: Der Hartree-Fock-Ansatz
Previous: Der Energie-Erwartungswert
Die Hartree-Fock-Gleichungen
Um zu einer Bestimmungsgleichung für die Orbitale 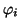 zu gelangen,
stationarisieren wir den Energie-Erwartungswert (49)
unter der Nebenbedingung, daß die Orbitale
zu gelangen,
stationarisieren wir den Energie-Erwartungswert (49)
unter der Nebenbedingung, daß die Orbitale 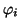 paarweise orthogonal
zueinander sein sollen
paarweise orthogonal
zueinander sein sollen
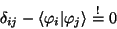 |
(52) |
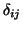 ist das Kronecker'sche Delta-Symbol
ist das Kronecker'sche Delta-Symbol
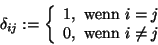 |
(53) |
Wir multiplizieren nun jede der Nebenbedingungen, Gln. (52),
mit einem noch zu bestimmenden Lagrange-Multiplikator
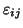 und addieren sie zum Energie-Erwartungswert (49)
und addieren sie zum Energie-Erwartungswert (49)
Wir wollen nun das Funktional G stationarisieren und können, wie in unserem
Beispiel, Abschnitt 2.1.3, sofort schreiben
Im letzten Schritt haben wir in den g-Integralen sowohl die Indizes
i und j,
als auch die Elektronenkoordinaten
r1 und
r2 vertauscht, um dann
offensichtlich gleiche Paare zusammenfassen zu können.
Wir definieren nun den sogenannten ``Fock-Operator,'' 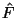 ,
durch seine Matrixelemente
,
durch seine Matrixelemente
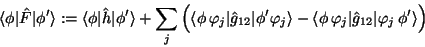 |
(56) |
und können die Gln. (55) schreiben als
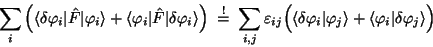 |
(57) |
Wie in unserem Beispiel (siehe Abschnitt 2.1.3) kann diese Gleichung
nur dann erfüllt sein, wenn für jedes Orbital 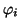 gilt
gilt
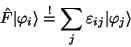 |
(58) |
und die entsprechenden konjugiert komplexen Gleichungen.
Die Hartree-Fock-Gleichungen (57) weisen nun aufgrund der Summe über
alle Orbitale eine Unbestimmtheit auf.
Dies muß auch so sein, denn man kann sich überlegen, daß eine
Slater-Determinante
(siehe Gln. [43]) invariant bezüglich einer beliebigen unitären
Transformation der Orbitale untereinander ist.
Man kann daher als zusätzliche Nebenbedingung fordern, daß die Matrix der
Lagrange-Multiplikatoren,
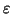 ,
diagonal ist, d.h. daß
gilt
,
diagonal ist, d.h. daß
gilt
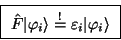 |
(59) |
mit den sog. ``Orbitalenergien''
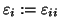 .
Man nennt diese Wahl der Orbitale, die ``kanonischen Hartree-Fock'' Orbitale
und die Glnn. (59), die ``kanonischen Hartree-Fock-Gleichungen.''
.
Man nennt diese Wahl der Orbitale, die ``kanonischen Hartree-Fock'' Orbitale
und die Glnn. (59), die ``kanonischen Hartree-Fock-Gleichungen.''
Da der Fock-Operator selbst von den Orbitalen, 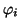 ,
abhängt,
ist die Gln. (59) eine nicht-lineare Eigenwertgleichung
und muß folglich iterativ gelöst werden.
Sind die Hartree-Fock-Gleichungen gelöst, dann stehen die Orbitalenergien
auf der Diagonalen der Fock-Matrix
,
abhängt,
ist die Gln. (59) eine nicht-lineare Eigenwertgleichung
und muß folglich iterativ gelöst werden.
Sind die Hartree-Fock-Gleichungen gelöst, dann stehen die Orbitalenergien
auf der Diagonalen der Fock-Matrix
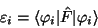 |
(60) |
Das Hartree-Fock-Verfahren, in der Literatur häufig mit HF abgekürzt, ist
das grundlegende Verfahren der Quantenchemie, mit dem sich in häufig
noch akzeptabler Genauigkeit, auch relativ große Moleküle behandeln lassen.
Es bildet weiter die (mathematische) Grundlage zu den, in letzter Zeit populär
gewordenen
Dichtefunktionalen.



Next: Ergänzung
Up: Der Hartree-Fock-Ansatz
Previous: Der Energie-Erwartungswert
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() ,
diagonal ist, d.h. daß
gilt
,
diagonal ist, d.h. daß
gilt
![]() ,
abhängt,
ist die Gln. (59) eine nicht-lineare Eigenwertgleichung
und muß folglich iterativ gelöst werden.
Sind die Hartree-Fock-Gleichungen gelöst, dann stehen die Orbitalenergien
auf der Diagonalen der Fock-Matrix
,
abhängt,
ist die Gln. (59) eine nicht-lineare Eigenwertgleichung
und muß folglich iterativ gelöst werden.
Sind die Hartree-Fock-Gleichungen gelöst, dann stehen die Orbitalenergien
auf der Diagonalen der Fock-Matrix