


Next: Der Hartree-Fock-Ansatz
Up: Variationsrechnung
Previous: Stationarisierung eines Funktionals
Beispiel: Rayleigh-Quotient ohne weitere Näherung
Als Beispiel für die Anwendung der Variationsrechnung wollen wir den
Rayleigh-Quotienten (27) ohne weitere Näherung stationarisieren.
Der Einfachheit halber fordern wir als Nebenbedingung, daß die Wellenfunktion
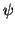 auf eins normiert ist und schreiben dies als
auf eins normiert ist und schreiben dies als
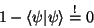 |
(36) |
Gemäß der Methode der Lagrange'schen Multiplikatoren versehen wir
die Nebenbedingung
mit einem noch näher zu bestimmenden Faktor E und addieren sie zum
Rayleigh-Quotienten
![\begin{displaymath}G[\psi] := \langle\psi\vert\hat H\vert\psi\rangle + E\big(
1 - \langle\psi\vert\psi\rangle
\big)
\end{displaymath}](img80.gif) |
(37) |
Das Funktional G muß nun unter der Berücksichtigung der Nebenbedingung
(36) stationarisiert werden.
Gemäß den Ausführungen in Abschnitt 2.1.2 können wir die
Variation von G in erster Ordnung bezüglich
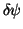 ,
also
,
also
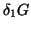 ,
sofort angeben und gemäß Gln. (35) erhalten wir
die Bedingung
,
sofort angeben und gemäß Gln. (35) erhalten wir
die Bedingung
![\begin{displaymath}
\delta_1 G[\psi] =
\langle\delta\psi\vert\hat H\vert\psi\ra...
...e +
\langle\psi\vert\delta\psi\rangle
\big) \stackrel{!}{=} 0
\end{displaymath}](img82.gif) |
(38) |
Diese Gleichung soll für beliebige Variationen
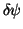 erfüllt sein.
Das kann aber nach dem sogenannten ``Fundamentalsatz der Variationsrechnung''
nur dann der Fall sein, wenn gilt
erfüllt sein.
Das kann aber nach dem sogenannten ``Fundamentalsatz der Variationsrechnung''
nur dann der Fall sein, wenn gilt
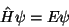 |
(39) |
bzw. wegen der Unabhängigkeit von
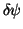 und
und
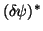 ,
die zu (39) konjugiert komplexe Gleichung.
Die Integrodifferentialgleichung (38) wird damit zur Eigenwertgleichung
(39) und wir erhalten als Ergebnis unserer Rechnung die Aussage, daß
der Rayleigh-Quotient (27) für die Eigenfunktionen des Hamilton-Operators
stationär ist.
,
die zu (39) konjugiert komplexe Gleichung.
Die Integrodifferentialgleichung (38) wird damit zur Eigenwertgleichung
(39) und wir erhalten als Ergebnis unserer Rechnung die Aussage, daß
der Rayleigh-Quotient (27) für die Eigenfunktionen des Hamilton-Operators
stationär ist.



Next: Der Hartree-Fock-Ansatz
Up: Variationsrechnung
Previous: Stationarisierung eines Funktionals
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.