Stationarisierung eines Funktionals

Um zu einer optimalen Wellenfunktion $\psi$ zu gelangen, kann man versuchen, einen geeigneten Ansatz $\psi$ für eine Wellenfunktion auszuwählen, und diesen so zu optimieren, daß der Rayleigh-Quotient (27) minimal wird.

  

Abbildung: Analytische Funktion in der Nähe eines Minimums

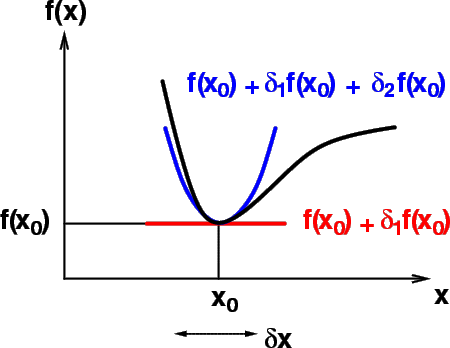
Betrachten wir zur Illustration das Verhalten einer analytischen Funktion in der Nähe eines Minimums (siehe Fig. 2.1.2). Am Minimum x₀ hat die Funktion den Wert f(x₀). Wir wollen das Verhalten der Funktion an einer beliebigen Stelle x bei einer, nicht notwendigerweise kleinen Verschiebung (``Variation'') $\delta x$untersuchen und entwickeln dazu die Funktion dort in eine Taylor-Reihe

$$f(x+\delta x) = f(x) + {df\over dx} \,\delta x + {1\over 2!}{d^2f\over dx^2}\,(\delta x)^2 + \ldots$$ (32)

Wir definieren nun die Variation der Funktion f, $\delta f$ als

$$\delta f \;:=\; f(x_0+\delta x) - f(x_0) \;=\; \delta_1 f + \delta_2 f + \ldots$$ (33)

mit

$$\delta_1 f := {df\over dx} \,\delta x, \quad \delta_2 f := {1\over 2!}{d^2f\over dx^2}\,(\delta x)^2, \quad \ldots$$ (34)

Wir erkennen (siehe Fig. 2.1.2), daß die erste Ableitung f' der Funktion f am Minimum x₀ verschwindet, d.h. eine notwendige Bedingung dafür, das f minimal wird ist, daß dort $\delta_1 f$, die Variation von f in erster Ordnung von $\delta x$ verschwindet.

Diese Bedingung läßt sich unmittelbar auf Funktionen mehrere Variablen und auf Funktionale erweitern. Die notwendige Bedingung dafür, daß ein Funktional $F[\psi]$ minimal wird, ist die Stationarität bezüglich einer beliebigen Variation $\delta\psi$

$$\delta_1 F[\psi,\delta\psi] \stackrel{!}{=} 0$$ (35)

wobei $\delta_1 F$ derjenige Anteil der Variation $\delta F$ ist, der bezüglich $\delta\psi$ von erster Ordnung ist.

  

Abbildung 4: Globales Verhalten einer analytischen Funktion

Das die Stationaritätsbedingung (35) auch für andere Fälle, als für das globale Minimum erfüllt sein kann, wird in Fig. 4 illustriert. Hier ist 1 das globale Minimum, 2 ein lokales Maximum, 3 ein höheres lokales Minimum und 4 kein Extremum sondern ein Umkehrpunkt. Bei Funktionen mehrerer Veränderlicher und bei Funktionalen können außerdem noch sogenannte ``Sattelpunkte'' auftreten, d.h. die Funktion ist an dieser Stelle lokal minimal in der einen, und lokal maximal in der anderen Richtung, d.h. der Funktionsverlauf ähnelt einem Sattel.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.