


Next: Stationarisierung eines Funktionals
Up: Variationsrechnung
Previous: Variationsrechnung
Variationsrechnung ist ein mathematisches Verfahren zum Lösen von bestimmten
Differentialgleichungen, wie sie z.B. in der klassischen Mechanik auftreten.
Im Fall der Schrödinger-Gleichung (26) definiert man zu diesem Zweck den
sogenannten ``Rayleigh''-Quotienten (nach Lord Rayleigh, einem Pionier der
klassischen Mechanik)
![\begin{displaymath}
F[\Psi] := {\langle\Psi\vert\hat H\vert\Psi\rangle \over \langle\Psi\vert\Psi\rangle}
\end{displaymath}](img56.gif) |
(27) |
Man nennt eine Funktion, die eine andere Funktion zum Argument hat, ein
``Funktional.''
Wir verwenden im folgenden die allgemein übliche Dirac'sche
Bracket-Notation.
In dieser Notation schreibt sich die Schrödinger-Gleichung (26)
als
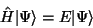 |
(28) |
Um zu einem Ausdruck der Form von Gln. (27) zu gelangen, projizieren
wir formal beide Seiten von links mit
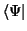
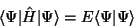 |
(29) |
Dies entspricht einer Multiplikation der beiden Seiten von Gln. (26)
von links mit 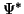 ,
dem konjugiert Komplexen von
,
dem konjugiert Komplexen von 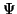 ,
und
einer anschließenden Integration über alle Koordinaten (der Elektronen).
Da E eine (reelle) Zahl ist, darf man sie vor das Integral ziehen.
,
und
einer anschließenden Integration über alle Koordinaten (der Elektronen).
Da E eine (reelle) Zahl ist, darf man sie vor das Integral ziehen.
Um physikalisch sinnvoll zu sein, muß (zumindest bei Grund- und niedrig
angeregten Zuständen) 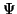 normierbar sein, d.h. es muß gelten
normierbar sein, d.h. es muß gelten
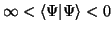 .
Daher dürfen wir beide Seiten durch
.
Daher dürfen wir beide Seiten durch
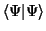 dividieren
und erhalten schließlich
dividieren
und erhalten schließlich
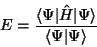 |
(30) |
Dies ist der bekannte Ausdruck für den (Energie-)Erwartungswert des
Hamilton-Operators.
Wir erkennen also, daß das Funktional (27) für die Lösungen 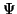 der Schrödinger-Gleichung (26) den jeweiligen, zu
der Schrödinger-Gleichung (26) den jeweiligen, zu 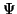 gehörenden
Eigenwert E annimmt.
Aber, im Gegensatz zu Gln. (26), erhalten wir
für beliebige, normierbare
gehörenden
Eigenwert E annimmt.
Aber, im Gegensatz zu Gln. (26), erhalten wir
für beliebige, normierbare 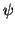 auch dann einen Zahlenwert für die
Energie, wenn die Gln. (26) nicht exakt erfüllt ist, was bei
Mehrelektronensystemen, bis auf unbedeutende Ausnahmen, stets der Fall
sein wird.
auch dann einen Zahlenwert für die
Energie, wenn die Gln. (26) nicht exakt erfüllt ist, was bei
Mehrelektronensystemen, bis auf unbedeutende Ausnahmen, stets der Fall
sein wird.
Man kann den Rayleigh-Quotienten nun dazu benutzen, um eine möglichst gute
Lösung der Schrödinger-Gleichung (26) zu finden.
Man kann zeigen, daß der Rayleigh-Quotient (27) eine
obere Schranke zum tiefsten Eigenwert E0 der
Schrödinger-Gleichung (26) ist, d.h.
![\begin{displaymath}F[\psi] :=
{\langle\psi\vert\hat H\vert\psi\rangle \over \lan...
...i\rangle} \geq E_0,\quad
\mbox{mit}\;\; \hat H\Psi_0=E_0\Psi_0
\end{displaymath}](img64.gif) |
(31) |
und daß die Gleichheit genau dann gilt, wenn
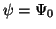 gewählt werden
kann.
Diesen Sachverhalt nennt man
``Variationstheorem''.
gewählt werden
kann.
Diesen Sachverhalt nennt man
``Variationstheorem''.



Next: Stationarisierung eines Funktionals
Up: Variationsrechnung
Previous: Variationsrechnung
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() normierbar sein, d.h. es muß gelten
normierbar sein, d.h. es muß gelten
![]() .
Daher dürfen wir beide Seiten durch
.
Daher dürfen wir beide Seiten durch
![]() dividieren
und erhalten schließlich
dividieren
und erhalten schließlich