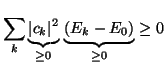Next: Die Slater-Condon-Regeln (für Fortgeschrittene)
Up: Anhang
Previous: Die Dirac'sche Bracket-Notation
Beweis des Variationstheorems
Wir nehmen ohne Beschränkung der Allgemeinheit an, daß unsere
genäherte Wellenfunktion 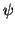 auf 1
normiert ist, d.h. daß
auf 1
normiert ist, d.h. daß
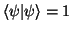 gilt.
Wir wollen nun zeigen, daß
gilt.
Wir wollen nun zeigen, daß
![\begin{displaymath}F[\psi] := \langle\psi\vert\hat H\vert\psi\rangle \geq E_0
\end{displaymath}](img250.gif) |
(115) |
Zu diesem Zweck entwickeln wir 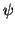 in die exakten, auf Eins normierten
Lösungen
in die exakten, auf Eins normierten
Lösungen 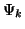 der Schrödinger-Gleichung (26)
der Schrödinger-Gleichung (26)
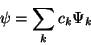 |
(116) |
(die Entwicklungskoeffizienten sind gegeben als
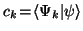 )
und setzen diesen Ausdruck in den Rayleigh-Quotienten (27) ein
)
und setzen diesen Ausdruck in den Rayleigh-Quotienten (27) ein
![\begin{displaymath}F[\psi] = \sum_{k,l} c^\ast_l\, c_k \,\langle\Psi_l\vert\hat H\vert\Psi_k\rangle
\end{displaymath}](img254.gif) |
(117) |
Wegen
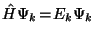 ergibt sich weiter
ergibt sich weiter
![\begin{displaymath}F[\psi] = \sum_{k,l} c^\ast_l\, c_k \,E_k\,\langle\Psi_l\vert\Psi_k\rangle
\end{displaymath}](img256.gif) |
(118) |
Man kann sich nun überlegen, daß verschiedene Lösungen der
Schrödinger-Gleichung orthogonal zueinander sind, wenn sie zu verschiedenen
Eigenwerten gehören und bei gleichen Eigenwerten, d.h. bei
Entartungen, orthogonal gewählt werden können und wir erhalten
unter Berücksichtigung von
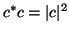
![\begin{displaymath}F[\psi] = \sum_k \vert c_k\vert^2 \,E_k
\end{displaymath}](img258.gif) |
(119) |
Wir überlegen uns nun, daß
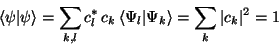 |
(120) |
und ziehen auf beiden Seiten E0 ab
Ist 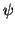 die exakte Lösung, dann verschwinden alle ck mit k>0,
ansonsten ergeben sich ausschließlich nicht-negative Summanden.
Somit folgt unmittelbar
die exakte Lösung, dann verschwinden alle ck mit k>0,
ansonsten ergeben sich ausschließlich nicht-negative Summanden.
Somit folgt unmittelbar
![\begin{displaymath}F[\psi] \;\geq\; E_0
\end{displaymath}](img264.gif) |
(122) |
was zu beweisen war




Next: Die Slater-Condon-Regeln (für Fortgeschrittene)
Up: Anhang
Previous: Die Dirac'sche Bracket-Notation
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() auf 1
normiert ist, d.h. daß
auf 1
normiert ist, d.h. daß
![]() gilt.
Wir wollen nun zeigen, daß
gilt.
Wir wollen nun zeigen, daß