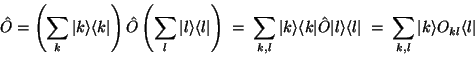Next: Beweis des Variationstheorems
Up: Anhang
Previous: Anhang
Die Dirac'sche Bracket-Notation
Nach Dirac schreibt man eine Wellenfunktion f als sogenannten ``Ket-Vektor''
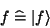 |
(109) |
Die dazugehörende konjugiert komplexe Funktion 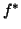 wird zum ``Bra-Vektor''
wird zum ``Bra-Vektor''
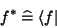 |
(110) |
Treffen ein Bra- und ein Ket-Vektor aufeinander, so wird daraus
(mit etwas Gewalt) ein ``Bracket'' (engl.: Klammer) und es wird
über die Koordinaten integriert
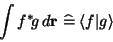 |
(111) |
Insbesondere schreibt man die Matrixelemente eines Operators 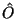 als
als
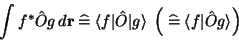 |
(112) |
Der senkrechte Strich auf der rechten Seite des Operator ist
optional.
Für Fortgeschrittene:
Man nennt Gln. (111) auch ``Hermite'sche Form.''
Häufig findet man dafür auch die Schreibweise (f,g).
Die Bezeichnung (Zustands-)Vektor für eine Wellenfunktion impliziert einen
Isomorphismus (
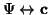 )
auf einen Vektorraum.
Der Übergang zwischen beiden Darstellungen erfolgt sehr elegant durch
die Zerlegung der Identität
)
auf einen Vektorraum.
Der Übergang zwischen beiden Darstellungen erfolgt sehr elegant durch
die Zerlegung der Identität
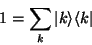 |
(113) |
wobei die
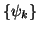 eine ortho-normale Basis zum jeweiligen
Definitionsbereich der verwendeten Operatoren sind.
Ein beliebiger Operator
eine ortho-normale Basis zum jeweiligen
Definitionsbereich der verwendeten Operatoren sind.
Ein beliebiger Operator 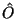 wird dann zu
wird dann zu
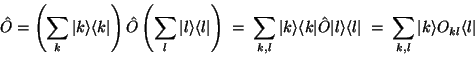 |
(114) |
D.h. ein Operator 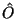 wird zu einer Matrix
O.
Weitere Einzelheiten findet man in einschlägigen Lehrbüchern der
linearen Algebra, z.B. bei Kowalski [11].
wird zu einer Matrix
O.
Weitere Einzelheiten findet man in einschlägigen Lehrbüchern der
linearen Algebra, z.B. bei Kowalski [11].



Next: Beweis des Variationstheorems
Up: Anhang
Previous: Anhang
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() )
auf einen Vektorraum.
Der Übergang zwischen beiden Darstellungen erfolgt sehr elegant durch
die Zerlegung der Identität
)
auf einen Vektorraum.
Der Übergang zwischen beiden Darstellungen erfolgt sehr elegant durch
die Zerlegung der Identität