Basisgrößen für die Untersuchung von Gasen sind neben
der Stoffmenge n und dem Volumen V, der Druck p (Kraft
pro Fläche) und die Temperatur T.
Bereits 1661 stellte der englische Physiker Robert
Boyle (1627-1691) experimentell fest, dass das Volumen einer
bestimmten Gasprobe dem Druck umgekehrt proportional ist. (Hier sind
die Originalarbeiten)
Das Boylesche Gesetz lautet
V ~ 1/p oder pV = konstant (bei konstantem n und T).
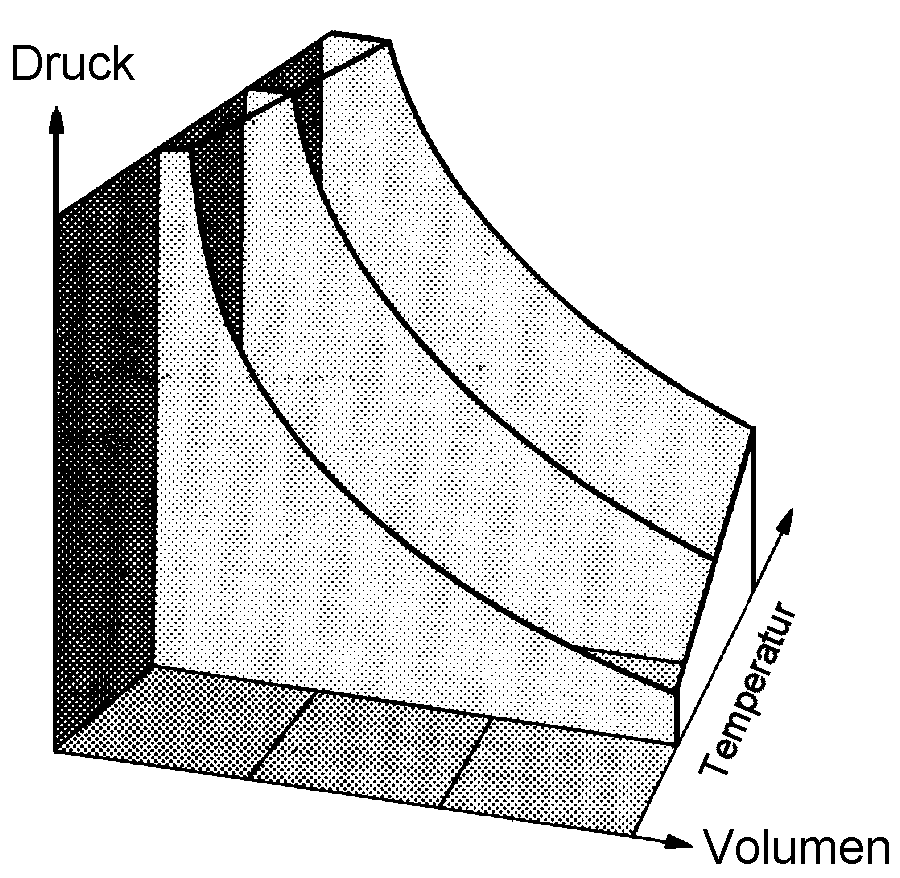 |
| Abb. 1: Die Abhängigkeit des Drucks vom Volumen für ein perfektes Gas bei drei verschiedenen Temperaturen (aber gleichen Mengen). Die Kurven sind Hyperbeln (p ~ 1/V) und heißen Isothermen. |
Will man dieses Gesetz auf molekularer Basis erklären, so geht man von der Überlegung aus, dass der Druck von den Stößen seiner Teilchen an die Gefäßwände herrührt. Halbiert man das Volumen, so verdoppelt man die Dichte; in der Folge stoßen in einem bestimmten Zeitraum doppelt so viele Teilchen an die Wände. Das bewirkt eine Verdopplung der mittleren Kraft, die das Gas ausübt, und damit auch eine Verdopplung des Druckes, ganz genau so, wie es das Boylsche Gesetz verlangt. Bei sehr kleinen Gasdichten sind die Teilchen so weit voneinander entfernt, dass die Kräfte, die sie aufeinander ausüben, im Mittel zu vernachlässigen sind. Auf diese Weise lässt sich der universelle Charakter des perfekten Gasgesetzes in dem Sinne verstehen, dass es für jedes Gas ohne Rücksicht auf seine chemische Zusammensetzung gilt.
Der Druck eines Gases bei festem Volumen, aber unterschiedlichen Temperaturen
wurde 1701 von Guillaume Amontons (franz. Chemiker, 1663-1705) untersucht.
Er fand, dass der Druck eine lineare Funktion von der Celsius-Temperatur
ist, p ~ t/°C + 273, so dass der extrapolierte Druck für
t »
-273 °C verschwinden muss. Er definierte auch eine absolute Temperaturskala.
Die Einheiten dieser Skala haben die gleiche Größe wie die Celsiusskala
und werden heutzutage Kelvin (K) genannt, T/K = t/°C + 273,15. Die
Beziehung p ~ T wurde von Joseph
Gay-Lussac (1778-1850) wieder veröffentlicht und trägt heute
seinen Namen (hier sind die Originalarbeiten)
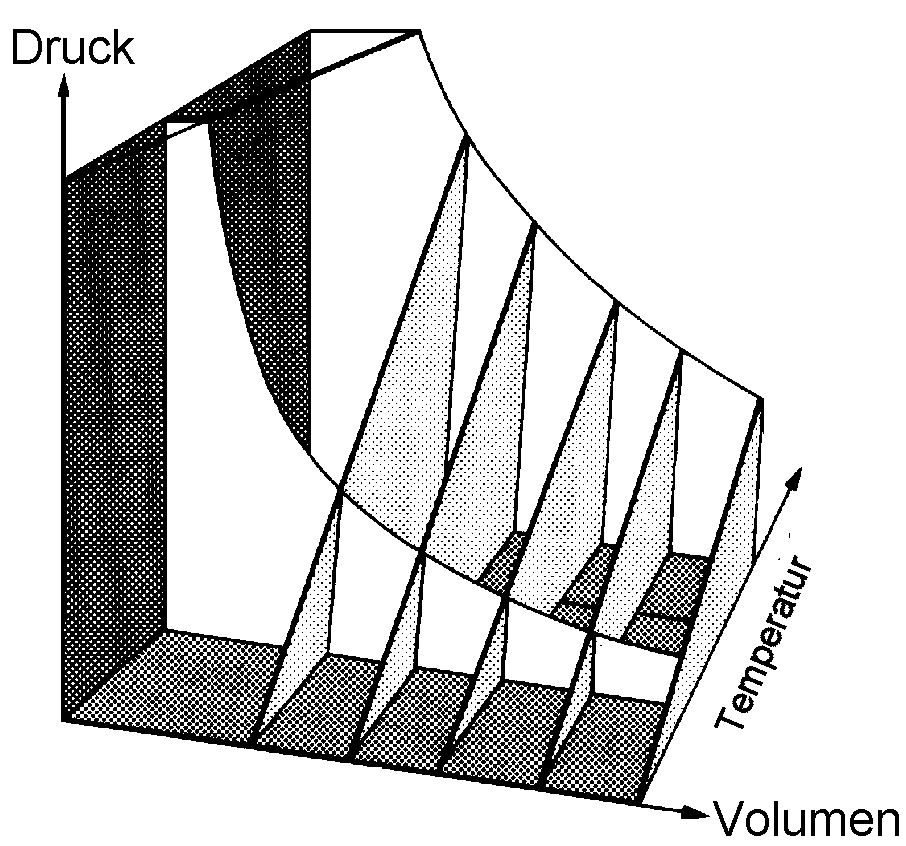 |
| Abb. 2: Die Abhängigkeit des Drucks von der Temperatur für ein perfektes Gas bei verschiedenen Volumina (aber gleichen Mengen). Die Geraden (p ~ T) heißen Isochoren. |
Bei konstantem Druck ist das Volumen und bei konstantem Volumen ist der Druck proportional zur Temperatur:
V ~ T (bei konstantem
n und p),
p ~ T (bei
konstantem n und V).
Auf molekularer Ebene hat eine Erklärung des Gay-Lussacschen Gesetzes davon auszugehen, dass eine Temperaturerhöhung die durchschnittliche Geschwindigkeit der Teilchen vergrößert. Wenn das Volumen dabei konstant gehalten wird, werden bei höheren Temperaturen mehr Teilchen und jedes einzelne (im Durchschnitt) mit einem größeren Impuls an die Wände stoßen; sie wirken also mit einer stärkeren Kraft und führen damit zu einem höheren Druck. Das der Druck linear von der Temperatur abhängt, wird verständlich, wenn wir uns mit der kinetischen Gastheorie befassen.
Die Temperaturabhängigkeit des Gasdrucks macht es möglich, Temperaturen zu messen, ohne Flüssigkeiten in Kapillaren einzusetzen. Weil sich jedes reale Gas im Grenzfall verschwindendes Druckes wie ein ideales Gas verhält, kann man stoffunabhängig mit Hilfe eines Gasthermometers mit konstantem Volumen die Temperatur messen. Dazu vergleicht man die beiden Drucke, die sich einstellen, wenn das Thermometer in thermischen Kontakt einmal mit der Probe, zum anderen mit einem Standard ist (als Standard nimmt man Wasser an seinem Tripelpunkt, an dem sich Eis, flüssiges Wasser und Wasserdampf miteinander im Gleichgewicht befinden). Beobachtet man, wenn das Gasthermometer mit der Probe in Kontakt ist, den Druck p, und, wenn es die Temperatur des Tripelpunktes von Wasser, T0, hat, den Druck p0, dann ist die Temperatur der Probe T ≈ (p/p0)T0. Nur wenn das Gas perfekt ist, gilt das genau; deshalb wiederholt man die Messungen mit immer kleineren Gasmengen im Thermometer und extrapoliert die Ergebnisse auf den Druck Null. Man kann dann normale, leichter handhabbare Thermometer an dem Gasthermometer eichen.
Der italienische Chemiker Amadeo Avogadro (1776-1856) stellte die Hypothese auf, dass gleiche Volumina von Gasen bei gleicher Temperatur und gleichem Druck dieselbe Anzahl von Teilchen enthalten. Weil die Anzahl der Teilchen proportional der Stoffmenge n ist, muss bei gegebener Temperatur und gegebenem Druck das Gasvolumen proportional zu n sein:
V ~ n (bei konstantem p und T).
Zusammenfassung der einzelnen Beobachtungen: Die Gaskonstante R
Die experimentellen Befunde V ~ 1/p, V ~ T und V ~ n kann man zu V ~ nT/p zusammenfassen. Die Proportionalitätskonstante wird Gaskonstante R genannt. Wir erhalten das Ideale Gasgesetz:
|
|
mit R = 8,31441 JK-1mol-1
Vm = V/n
|
|
Als Standardwerte für Druck und Temperatur (Abkürzung STP) wurden früher allgemein 0°C und 101325 Pa (= 1013,25 mbar = 1 atm) gewählt. Unter STP-Bedingungen hat das Molvolumen eines perfekten Gases den Wert 22,414 dm3mol-1. Inzwischen wurde vorgeschlagen, als Standardbedingungen die Werte 298,15 K und 100000 Pa = 1 bar festzulegen. Diese Bedingungen werden SATP (Standard Ambient Temperature and Pressure) genannt. Das perfekte Gas hat unter diesen Bedingungen ein Molvolumen von 24,789 dm3mol-1.
Historisch bedingt gibt es viele Einheiten für den Druck. Er sollte ausschließlich in Pascal angegeben werden. Die Studierenden in den USA verbringen viele Stunden damit, "ihre Einheiten", nämlich psi (pounds per square inch = 0,451 kg/2,542cm2) in [N/m2] umzurechnen. Ältere "krumme Einheiten" sind Torr (760 torr = 1 atm), mmHg (1 mmHg = 1 torr), atm ( 1 atm = 101 325 Pa) und bar ( 1 bar = 100 000 Pa), wobei die Mediziner weiterhin beim Blutdruckmessen in mmHg angeben.
Die kleinste Stoffmenge ist das Teilchen, das die Identität des
Stoffes bewahrt. Es kann ein Atom, ein Molekül oder ein Ion sein.
Ein Mol einer Substanz besitzt genauso viele "Einheitsteilchen" wie die
Anzahl Atomen in 12 g des Kohlenstoffisotops 12C enthalten sind.
Die Anzahl N von "Einheitsteilchen" einer beliebigen Substanzmenge n ist
dann
| N = NA · n |
Die Konstante NA ist die Loschmidtsche Zahl oder auch Avogadrokonstante.
Der experimentell bestimmte Wert beträgt:
| NA = 6,02214 · 1023 mol-1 |
Das ideale Gasgesetz kann nun bzgl. der Anzahl von Gasteilchen umgeschrieben
werden:
| pV = N · kT |
wobei wir zur Abkürzung die Boltzmannkonstante k eingeführt
haben:
| R = k · NA |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.