Es folgen die Ergebnisse für die Eigenwerte und Funktionen des Drehimpulses zum Quadrat und der z-Komponente des Drehimpulses. Die Berechnung, die auch Kenntnisse über Vertauschungsrelationen erfordert, gibt's hier. Für die Eigenwerte erhält man:
| L² Yl,m
= l (l +1) Lz Yl,m
= m |
− l ≤ m ≤ l |
Die Berechnung zeigt, dass sich m nur um ganzzahlige Werte ändern kann. Da der kleinste Wert von m (m = - l) dem Betrage nach dem größten Wert von m (m = l) entspricht, kann l nur halb- oder ganzzahlig sein. Bei gegebenem l gibt es also 2l + 1 Werte für m. Halbzahlige Werte entsprechen dem Spin. Die entsprechenden Eigenfunktionen sind nicht als Ortsfunktionen darstellbar und sind nicht aus der Schrödingergleichung ableitbar. Die halbzahligen Drehimpulseigenwerte ergeben sich nur durch eine Operatorbehandlung des Drehimpulses. Widmen wir uns daher zunächst den ganzzahligen Eigenwerten, d.h. l kann die Werte 0,1,2,3,... annehmen und m beginnt bei m = -l und läuft in Einerschritten hoch bis m = +l.
|
L² Yl,m
= l (l +1) Lz Yl,m
= m |
Die Eigenfunktionen der z-Komponente des Drehimpulses hängen nur vom Winkel j ab, so dass wir den folgenden Separationsansatz wählen können:
| Yl,m(J,j) = | P(J) | · | φ(j) |
| f(j) = (2π)-½ eimj |
Die Funktionen bzgl. J heißen für
m = 0 Legendresche
Polynome (Pl(cosJ))
und für m ¹ 0 zugeordnete
Legendresche Polynome (Pl,m(cosJ);
manchmal schreibt man den Index für m auch oben: Plm(cosJ)).
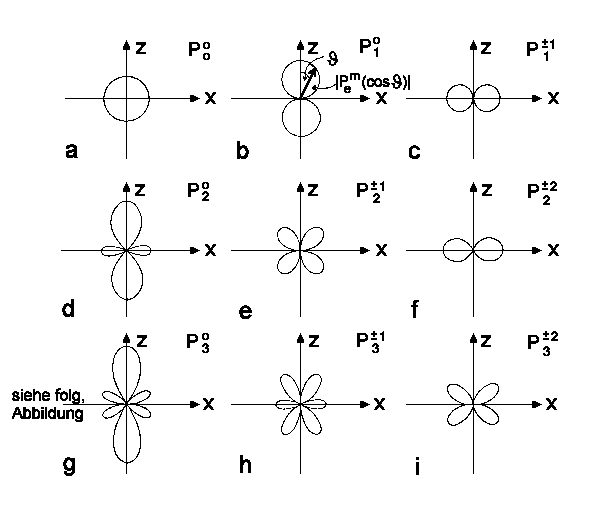
In der folgenden Darstellung sind alle Legendreschen Polynome Plm(cosJ)
bis l =3 in Polarkoordinaten dargestellt. Dabei wird der Absolutbetrag einer Funktion, die von einem Winkel abhängt, als Radiusvektor unter diesem Winkel relativ zur z-Achse aufgetragen. Zur Erinnerung:
| So sieht ψ = sin α ... | |
... in gewöhnlicher Auftragung ...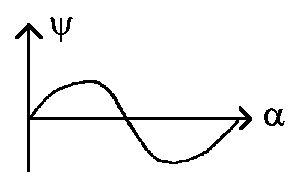 |
... und so in Polardarstellung aus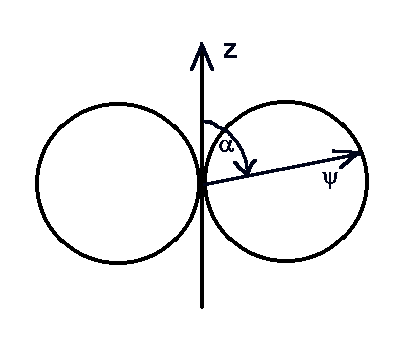 |
 |
|
|
Abb.1a-k: Polarkoordinatendarstellung
der J-Abhängigkeit
Legendre Polynome (a,d,g) und zugeordnete Legendre Polynome. Zur Veranschaulichung der Funktionen Plm(cosJ) ist in der Richtung des Radiusvektors, der mit der z-Achse den Winkel J einschließt, der jeweilige Betrag von Plm(cosJ) abgetragen. |
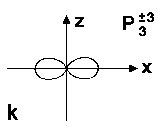 |
siehe Abb.1g-k für P3m |
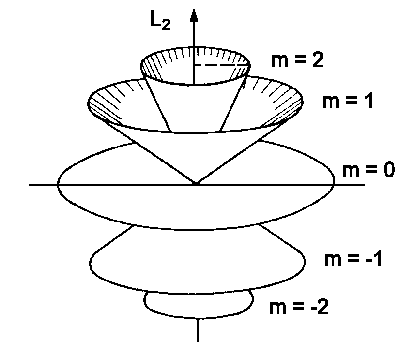
| Abb.2: Richtungsquantisierung: Die Einstellungsmöglichkeit des Drehimpulses L mit der Drehimpulsquantenzahl l = 2 |
Die gesamte Funktion Yl,m(J,j)
= P(J)·f(j)
heißt Kugelflächenfunktion.
Die Normierung für die Kugelflächenfunktionen erfolgt durch Integration über das entsprechende ("Winkel") Volumen dW
= sinJ dJ
dj:
| o∫2π | oòp | |Yl,m|² | sinJ dJ dj | = 1 |
| j | J | |¾¾¯¾¾| | ||
| dΩ | ||||
|
Yl,m(J,j)
= Plm(cosJ)·φm
(j) φm(j)
= 1/(2π)½ eimj
|
||||
| Elektron | l | m | Yl,m(J,j) | Yl,m Yl,m* |
| s | 0 | 0 | 1/(4π)½ | 1/4p |
| p | 1
1 |
±1
0 |
-/+(3/8p)½
sinJ e±ij
(3/4p)½ cosJ |
3/8p
sin²J
3/4p cos²J |
| d | 2
2 2 |
±2
±1 0 |
(15/32p)½
sin²J e±2ij
-/+(15/8p)½ sinJcosJ e±ij (5/16p)½ (3cos²J − 1) |
15/32p
sin4J
15/8p sin²Jcos²J 5/16p (3cos²J- 1)² |
| f | 3
3 3 3 |
±3
±2 ±1 0 |
-/+(35/64p)½
sin3J e±3ij
(105/32p)½ sin²JcosJ e±2ij -/+(21/64p)½ sinJ (1 - 5 cos²J) e±ij (7/16p)½ (5 cos3J − 3 cosJ) |
35/64p
sin6J
105/32p sin4Jcos²J 21/64p sin²J (1 - 5 cos²J)² 7/16π (5 cos3J − 3 cosJ) |
| g | 4
4 4 4 4 |
±4
±3 ±2 ±1 0 |
(315/512p)½
sin4J e±i4j
-/+(315/64p)½ sin3JcosJ e±3ij (225/660p)½ sin²J (7 cos²J- 1) e±2ij -/+(225/320p)½ sinJ (7 cos3J- 3 cosJ) e±ij (9/256p)½ (35 cos4J − 30 cos²J + 3) |
315/512p
sin8J
315/64p sin6Jcos²J 225/660p sin4J (7 cos3J- 1)² 225/320p sin²J (7 cos3J- 3 cosJ)² 9/256π (35 cos4J − 30 cos²J + 3)² |
Die Gleichungen für die Kugelflächenfunktion eignen sich äußerst schlecht für eine graphische Darstellung, wegen des Imaginäranteils im Exponenten bzgl. der j-Abhängigkeit:
Um das "i" los zu werden, wendet man einen Trick an: Die f-Funktionen sind entartete Eigenfunktionen (da es zu einem l-Eigenwert mehrere m-Werte gibt (außer bei l=0)). Und dann gilt noch ganz allgemein:
| Jede Linearkombination entarteter Eigenfunktionen χi
ist wieder eine Eigenfunktion zum entsprechenden Operator:
f = c1 χ1 + c2 χ2 → Linearkombination F χ1 = Fe χ1 und Fχ2 = Fe χ2 Entartet, d.h. gleicher Eigenwert Fe für beide Funktionen χ1 und χ2 F f = c1 F χ1 + c2 F χ2 = Fe (c1 χ1 + c2 χ2) = Fe f
q. e. d. |
Man benutzt daher spezielle Linearkombinationen der beiden Funktionen e+i|m|j
und e−i|m|j, um
das "i" zu eliminieren:
und erhalten nach Normierung die reellen Funktionen (man
beachte, dass jede Multiplikation mit -1,i,-i nichts ändert):
| f+ =
1/p½
cos
mj f- = 1/p½ sin mj |
So können wir reelle Funktionen erzeugen, die für chemische Betrachtungsweisen äußerst nützlich sind. In der folgenden Tabelle sind die Funktionen für l und |ml| aufgeführt:
| l | ml | Winkelfunktion |
| 0 | 0 | s = 1/(4π)½ |
| 1 | 0 | pz = (3/4π)½cosJ |
| +1 / -1 | px = (3/4π)½sinJcosj | |
| py = (3/4π)½sinJsinj | ||
| 2 | 0 | d3z²−r² = (5/16π)½(3 cos²J - 1) |
| +1 / -1 | dxz = (15/4π)½sinJcosJcosj | |
| dyz = (15/4π)½sinJcosJsinj | ||
| +2 / -2 | dx²−y² = (15/16π)½sin²Jcos2j | |
| dxy = (15/16π)½sin²Jsin2j |
Die Zustände mit unterschiedlichem l werden aus historischen Gründen mit folgenden Buchstaben gekennzeichnet:
l = 0,1,2,3,4,5,6,7,8,...
s,p,d,f,g,h,i,k,l,...
Der niedrigste s-Zustand (l = 0) ist isotrop; weist also sphärische Symmetrie auf. Im Polardiagramm bedeutet dies, dass man eine Kugelschale bekommt, da der Wert der s-Funktion (angezeigt durch die Länge einer Geraden vom Ursprung) in alle Richtungen (J, j) gleich ist. Dies ist verständlich, da für den Drehimpuls Null keine Orientierung der Elektronenbewegung bevorzugt ist.
Für l = 1, also p-Zustände, gibt es drei Winkelfunktionen px, py, pz, die eine bevorzugte Bewegung des Elektrons entlang der drei Koordinatenachsen beschreiben und daher für eine Beschreibung der chemischen Bindung sehr wichtig sind.
Für l = 2, also d-Zustände, gibt es fünf Winkelfunktionen, die etwas aufwendiger in ihrer Darstellung sind. Für noch größere Werte von l (g, h, j...) wird es entsprechend komplizierter. Ein Mathematica-Programm hilft hier.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.