 |
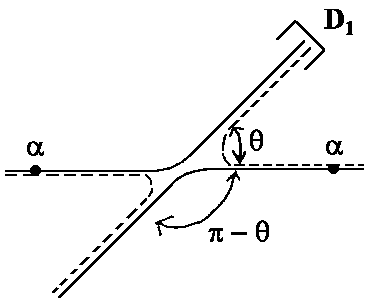 | ||
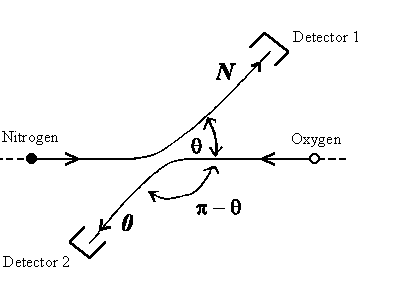
| The probability P(θ) of detecting a particle at angle θ depends on the dispersion amplitude f(θ) for | |||
| distinguishable particles: | non distinguishable particles: | ||
An example here are nitrogen and hydrogen atoms. |
An example is α-particles (helium nuclei, He++)
| ||
| For dispersion angle θ = π/2 it's obviously f(θ) = f(p - q), i.e.: | |||
| Pd(θ=π/2) = ½f(θ=π/2)½2 +½f(θ=π/2)½2
= 2½f(θ=π/2)½2 |
Pi(θ=π/2)
=½f(π/2) + f(π/2)½2
= 4½f(π/2)½2 | ||
Unfortunately, it's more complicated if we observe dispersion of
identical electrons. The following will result in this case:
|
|
|
|
We previously thought that electrons are identical. Scientists tried dilligently to find any characteristic of electrons that would help them distinguish between two different electrons. The internal characteristic that they found is called Spin! (Stern-Gerlach Experiment). We now know that there are two "sorts" of electron, i.e. spin can take only two states which we will designate as spin up and spin down. Electrons with differing spins have the same features in diffraction experiment, i.e. there is no special identification characteristic with which one can identify different electron and therefore it's necessary:
Pi = ½f(θ) − f(p-q)½2.
If a spin up electron collides with a spin down electron,the particles are distinguishable and we can write:
Pd = ½f(θ)½2+½f(p-q)½2
An electron has spin s = 1/2 (both projections are possible ms = +1/2 and ms = -1/2 for spin up and spin down). Spin values can vary for other particles but it's always a multiple of 1/2. Therefore, all particles are divided into 2 classes:
Bose particles
(integer spin): f(θ) + f(p -
q) [α-particles, photons]
Fermi particles (half-integer spin):
f(θ) − f(p - q)
[electrons, muons]
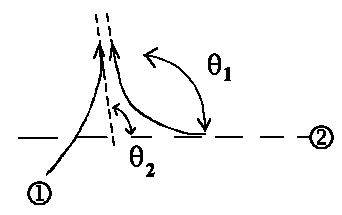
Pi = ½f(θ1) − f(θ2)½2
If both particles move in the same direction then it should be θ1
= θ2 or finally
| Pi = 0 !!! |
Hence two electrons with the same spin can't be in the same state. This is the well-known Pauli exclusion principle (Wolfgang Pauli).
We will see the concept of electron spin later when we study atomic and molecular spectroscopy. However, we now return again to the double slit experiment in order to describe sudden behavior of a particle using more comprehensive mathematics. Moreover we will again usestrange angle brackets and wavefunctions.
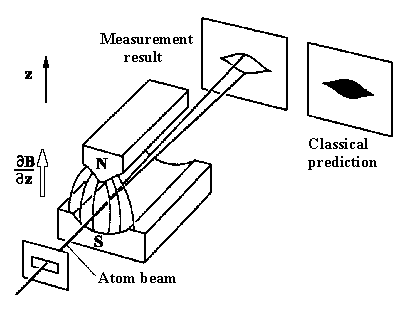 |
| The Stern-Gerlach experiment schematic layout: the atomic beam comes through a homogeneous magnetic field. One observes fragmentation of the incident beam into 2 components which are designated as spin up and spin down. We observe a uniformly filled area (as it is shown on the left part of this figure). |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.