Summarization and explanation of (2) - Molecular Hydrogen

In the previous unit, we applied our quantum mechanical approach to solve a problem which was very pressing in 19th century: understanding the structure of benzene. Evidence showed benzene to have C-C-bonds of equal length, which was difficult to explain. In addition to benzene, describing a system of electrons and nuclei with combined wave functions will also be useful in the most fundamental cases of molecular bonding. One example is molecular hydrogen which consists of a pair of electrons moving around two surrounding protons. To begin, we will consider the simplest molecule imaginable. This molecule can be created, in principle, by bonding one proton to a Hydrogen atom. Electrostatic principles state that there is only repulsion between the two protons of the resulting molecule. It would be interesting to find out if the lone electron could serve as a 'glue' between the two repulsive protons, thereby forming a stable system of three particles. If successful, our theory will support the idea that the cationic molecule H2+ is stable.

1. The H2+molecule

If we imagine a proton being pushed into the sphere of one hydrogen atom, we will reach a point where the electron does not belong to just one proton anymore. Such an exchange goes along with the exchange energy or interaction

Basic states Linear combination
|I> 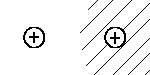In analogy to benzene, the electron's wave function in the H2 cation is described by |I> and |II> which are combination of the basic states.
|II>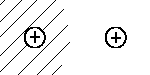

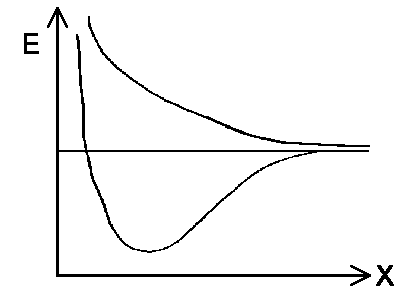
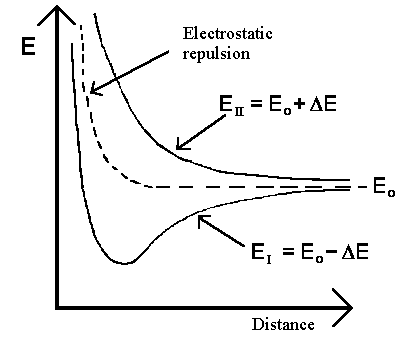The solution with the lowest energy for the whole system is characterized by a wavefunction with equal amplitude in the proximity of both protons. The total energy is equal to EI =  Eo- ΔE in state |I>. The dependency between the two protons' distance and energy energy is shown in the diagram to the left. The interaction ΔE increases if the protons get closer to each other. It further suggests that the previously mentioned quantum mechanical exchange energy overcompensates for the repulsive forces between the two protons and is fundamental for chemical bonding. Note that the same exchange energy would destabilize the system of the particles in state  |II>.

2.) The hydrogen molecule H2

Basic states
If we have a pair of electrons, they might as well be exchanged between protons and with respect to the system's energy. One could assume that the extent of energy splitting for this system of four particles would be even more pronounced.  At this point, we have to pay attention to the nature of electrons. In quantum mechanics, they are classified as Fermi particles. Therefore, if the two electrons have equal spins, i.e. are undistinguishable, and are renamed, the new wave function must reverse its sign.

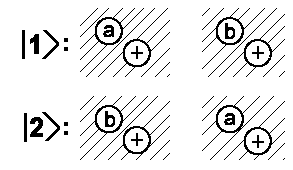If we use |I> = 1/√2 (|1> + |2>) as linear combination, we will obtain |I'> = 1/√2 (|2> + |1>) = |I>. No change of sign occurs. Consequently, if both electrons' spin are equal, there is only one possible state |II> = 1/√2 (|1> − |2>) since electron exchange yields: |II'> = 1/√2 (|2> − |1>) = −|I>.

Because of the higher energy of this state |II> both H atoms will repulse each other. There is no H2 molecule with parallel spins. If both electrons have spins pointed to opposite directions, then then the molecule has a stable state. The total spin of  this molecule is essentially equal to zero for this state.

Such two electron binding leads to the usual valence bonding. Nevertheless, the above-mentioned considerations hold true even in situations where the electrostic attraction of one of the nuclei is greater (for instance, NaCl). All possible gradations of bindings between covalent and ionic can be explained using the model of the two electron system. 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.