Nuclear Magnetic Resonance (NMR) Spectroscopy

Introduction

Nuclear magnetic resonance (NMR) spectroscopy uses radiofrequency radiation to induce transitions between different nuclear spin states of samples in a magnetic field. NMR spectroscopy can be used for quantitative measurements, but it is most useful for determining the structure of molecules (along with IR spectroscopy and mass spectrometry). The utility of NMR spectroscopy for structural characterization arises because different atoms in a molecule experience slightly different magnetic fields and therefore transitions at slightly different resonance frequencies in an NMR spectrum. Furthermore, splittings of the spectra lines arise due to interactions between different nuclei, which provides information about the proximity of different atoms in a molecule.

General Principles

Nuclei with an odd number of protons, neutrons, or both, will have an instrinsic nuclear angular momentum or "nuclear spin".
Spin quantum number for various nuclei
Number of protons Number of Neutrons Spin Quantum Number (I) Examples
Even Even 0 12C, 16O, 32S
Odd Even 1/2  1H, 19F, 31P
" " 3/2 11B,35Cl, 79Br, 127I
Even Odd 1/2 13C
" " 5/2 17O
Odd Odd 1 2H, 14N

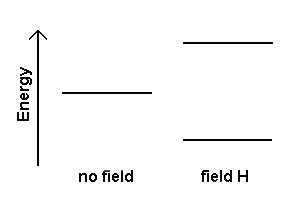
When a nucleus with a non-zero spin is placed in a magnetic field, the nuclear spin can align in either the same direction or in the opposite direction as the external magnetic field. A nucleus that has its spin aligned with the external field will have a lower energy than when it has its spin aligned in the opposite direction to the field. Thus, these two nuclear spin alignments have different energies and application of a magnetic field results in an energy level diagram like:

Nuclear magnetic resonance (NMR) spectroscopy uses the transition between these levels to detect and quantify nuclei. The magnitude of the energy splitting between these levels for nuclei in a strong magnetic field is in the range of radiofrequency (RF) radiation. Absorption of the RF radiation causes nuclear spins to realign or flip in the higher-energy direction. After absorbing energy, nuclei will reemit RF radiation and return to the lower-energy state.

The energy (and thus frequency) of an NMR transition depends on the magnetic-field strength and a proportionality factor for each nucleus called the magnetogyric ratio, γ. The frequency of a transition is given by:

ν  =  γ/2π H

where ν is the frequency of the resonant radiation and H is the strength of the magnetic field.

Chemical Shift

The local environment around a given nucleus in a molecule perturbs the local magnetic field that is exerted on that nucleus. Since the resonance frequency of the transition, nuclei in different environments have slightly different transition energies. This dependence of the transition energy on the position of a particular atom in a molecule gives NMR spectroscopy it's utility for structural characterization.

The resonance frequencies of different nuclei in an atom are described by a relative shift compared to the frequency of a standard. This relative shift is called the chemical shift, δ, and is given by:

δ  =  [(νsample- nref)/νref)] 1·106

where δ has units of ppm. For 1H NMR spectroscopy the reference compound is tetramethylsilane, Si(CH3)4, or TMS.

Instrumentation

There are two NMR spectrometer designs, continuous-wave (cw), and pulsed or Fourier-transform (FT-NMR). Pulsed FT-NMR instruments have largely replaced cw-NMR spectrometers. Due to the lower maintenance and operating cost of cw instruments, they are still used for routine 1H NMR spectroscopy at 60 MHz. (Low-resolution cw instruments require only water-cooled electromagnets instead of the liquid-He-cooled superconducting magnets found in higher-field FT-NMR spectrometers.) These two spectrometer designs are described in separate cw-NMR and FT-NMR documents.

For more extensive information and resources on NMR spectroscopy please see Scott van Bramer's NMR pages.
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.