Das Wasserstoffmolekül-Ion H₂⁺

Eine besonders einfache Form nimmt die LCAO-Entwicklung bei homonuklearen zweiatomigen Molekülen an; das sind Moleküle mit gleichen Atomen, wie beispielsweise H₂, O₂, N₂ usw. Es empfiehlt sich, mit dem einfachsten dieser Systeme zu beginnen, dem Wasserstoffmolekül-Ion H₂⁺. Da dieses Molekül-Ion nur ein Elektron enthält, hat seine Betrachtung dieselbe zentrale Bedeutung für Moleküle wie die des Wasserstoffatoms für die Struktur der Atome im Periodensystem.

Dabei beachten wir, dass in den beiden Säkulargleichungen die Größen α_A und α_B gleich sein müssen. Die beiden Enden des Moleküls sind nämlich nicht unterscheidbar und ein Elektron hat in φ_A (an einem Kern) dieselbe Energie wie in φ_B (am anderen Kern). Setzten wir folglich α_A = α_B = α, so lauten die Säkulargleichungen:
 

die nur dann eine "chemisch sinnvolle" Lösung (d.h. c_A und c_B ungleich Null) besitzen, wenn die Energie die beiden Werte
 

annimmt (Herleitung). Ganz einfach wird es, wenn S sehr klein gegenüber 1 ist:
 

Bei "etwas größerem S" gilt in besserer Näherung:   E_± @ a ± (b - aS)

Die Gleichungen zeigen, wie sich ein ursprünglich entartetes Paar von Energiewerten α in zwei verschiedene Werte aufspaltet und zwar symmetrisch bezgl. des ursprünglichen Energiewertes, falls S klein gegen 1 ist. Der eine neue Energiewert liegt dann höher und der andere niedriger als zuvor. Man erkennt auch, dass die Größe der Aufspaltung durch den Wert (b-aS) bestimmt ist. Das MO mit der tiefsten Energie wird bindendes MO genannt, denn dessen Energie ist kleiner als die des Wasserstoffatoms, und dieses stellt den Grundzustand des Moleküls dar. Das andere MO mit der höheren Energie ist das antibindende MO; dessen Energie ist größer als die des Wasserstoffatoms. Die Ergebnisse sind im folgenden Bild schematisch dargestellt. Eine Asymmetrie der Aufspaltung tritt nur dann auf, wenn S nicht gegen 1 vernachlässigt wird.
 

Um nun die Wellenfunktion y = c_Aφ_A + c_Bφ_B für die Energiezustände zu bestimmen, benötigen wir noch die Koeffizienten c_Aund c_B. Durch Einsetzen der beiden Energiewerte E_± in die Säkulargleichungen erhalten wir die beiden Lösungen für die Koeffizienten: c_A = ± c_B. Die entsprechenden Molekülorbitale sind dann:
 

wobei die c_A - wie üblich - über die Normierung (s.u.) bestimmt werden.

Die sich so ergebenden Wellenfunktionen y+ und y- sowie deren Betragsquadrat |y+|² und |y-|² kann man sich für das H₂⁺-Ion durch anklicken ansehen.

Für den weiteren Verlauf der Rechnung verwenden wir für φ_A und φ_B die Form als 1s-AO für das Wasserstoffatom; damit können wir dann α, β und S für jeden vorgegebenen interatomaren Abstand R berechnen. Auf diese Weise erhalten wir die elektronische Energie, und wenn wir dazu noch die Energie der Kernabstoßung ^e²_/4peoR addieren, so erhalten wir die Energiekurve für das Molekül.
 

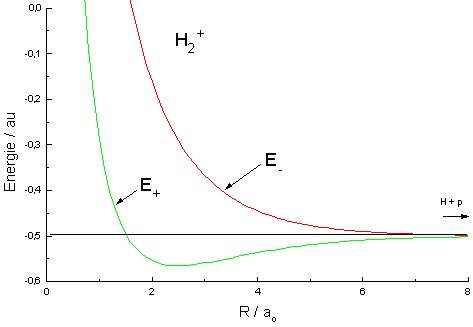Abb.1: Verlauf der (absoluten) Energie für das bindende (+) und das antibindende MO (-)  als Fkt. des internuklearen Abstandes R. Alles in atomaren Einheiten: ao = Bohrscher  Radius, Energie/au: 1au = zweifache Ionisierungsenergie des Wasserstoffatoms.

Die Ergebnisse sind in der nebenstehenden Abbildung dargestellt. Die Energiekurve für y₊ ist die für den Grundzustand des Moleküls. Aus diesen Energiekurven folgen einige Eigenschaften des Moleküls:

• Zunächst hat die Kurve für y₊ ein Minimum bei einem Kernabstand von etwas mehr als 2a_o (etwa 100pm). Daraus folgt, dass das H₂⁺ stabil sein muss, wobei die berechnete Bindungsenergie etwa 1,77 eV beträgt, während der experimentelle Wert bei 2,77 eV liegt. Gar nicht so schlecht das Ergebnis! Jetzt wissen wir also, wie wir die Energiekurve eines Moleküls, das experimentell bekannt ist, näherungsweise berechnen können.
• Dann ist zu erwähnen, dass die Energiekurve für y_- kein Minimum aufweist, so dass das Molekül in diesem Zustand instabil und spontan unter Energieabgabe in H und ein Proton p (H⁺) zerfällt.

Energiekurven dieser Art nennt man "anziehend" und "abstoßend", und dementsprechen heißen die Molekülorbitale "bindend" und "antibindend". Das ist schon fast Moleküldynamik! Denn wenn wir "unser" Wasserstoffion vom bindenden ins antibindende Orbital anregen, dann zerfällt das Ion:  H₂⁺ + hn ® H+H⁺

Noch etwas Mathe zum H₂⁺

Die Normierung (d.h. unser Elektron im gesamten Raum zu finden) muss 1 sein:

ò |y₊|² = 1 = _∫ c_A(φ_A+ φ_B)·c_A(φ_A+ φ_B) = c_A²( _ò |f_A|² + _∫2|φ_Aφ_B| + _∫ |φ_B|² )
                                                                            ¯               ¯             ¯
                                                                            1              2S             1

bindend:        c_A² = ¹/_[2(1+S)];  y₊ = (φ_A + φ_B)_/Ö[2(1+S)]
antibindend:  c_A² = ¹/_[2(1-S)];   y_- = (φ_A - f_B)_/Ö[2(1-S)]

Die Wahrscheinlichkeitsdichte P ist danach P = ( |f_A|² +2|φ_Aφ_B| +|φ_B|² )/[2(1+S)], d.h. die "Ladungsdichte des Elektrons" ist pro Kern 1/[2(1+S)] und 1/(1+S) dafür, dass das Elektron zu beiden Kernen gehört und damit die Bindung macht.

Mathematica-Besitzer können sich leicht selber die Funktionen y+ und y- sowie deren Betragsquadrat |y+|² und |y-|² darstellen (auch für beliebige internukleare Entfernung Rgl):

Rgl=2.4;
psiP=Exp[-Sqrt[x^2+y^2]/2]+Exp[-Sqrt[(x-Rgl)^2+y^2]/2]
psiM=Exp[-Sqrt[x^2+y^2]/2]-Exp[-Sqrt[(x-Rgl)^2+y^2]/2]
Plot3D[psiM, {x,-4,6}, {y,-4,4}, PlotPoints -> 50, PlotRange -> All]
Plot3D[psiP, {x,-4,6}, {y,-4,4}, PlotPoints -> 50, PlotRange -> All]
Plot3D[psiP^2, {x,-4,6}, {y,-4,4}, PlotPoints -> 50, PlotRange -> All]
Plot3D[psiM^2, {x,-4,6}, {y,-4,4}, PlotPoints -> 100, PlotRange -> All]

Der Hamilton-Operator für das H₂⁺ lautet: H  = -  ^h²/_2mD +^e/_4peo [- ¹/r_A - ¹/r_B + ¹/_R]
oder in sogenannten atomaren Einheiten (au): H  = - ½ D - ¹/r_A - ¹/r_B + ¹/_R
Beim H-Problem gilt: ( -½Δ - ¹/r_A) φ_A = - ½ φ_A     [Grundzustand Energie in au]

α = òf_A^*Hφ_Adτ. Aus H-Problem wissen wir:  Hφ_A = (- ½Δ - ¹/r_A - ¹/r_B + ¹/_R)φ_A = - ½ φ_A + (- ¹/r_B + ¹/_R)φ_A

α = -½ +  ∫φ_A* (- ¹/r_B + ¹/_R)φ_Adτ = -½ + J

ß  =  òf_B* Hφ_Adτ = − ½ òf_B*φ_Adτ + ∫ φ_B* (- ¹/r_B + ¹/_R)φ_Adτ = -½ S + K

und dem Überlappungsintegral  S = - òf_B*φ_Adτ
 

Für 1s-Orbitale erhalten wir:
    S  =  e^-R (1 + R + R²/3)
    J  =  e^-2R (1 + ¹/_R)
    K =  ^S/_R - e^-R(1 + R)  =  e^-R[¹/_R - ²/₃R]
 

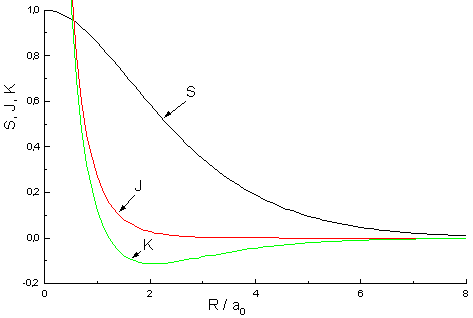Abb.2: Werteverlauf des Überlappungsintegral S, Coulombintegral J und Austauschintegral K

Und so leicht findet man das Minimum von E₊ mit Mathematica (Ableitung  Nullsetzen und nach R auflösen):

DEpl=D[Epl,R];
FindRoot[DEpl==0,{R,{1.5,2.5}}]

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.