Hückel

Die Berechnung der Molekülorbitale nach Hückel (Erich Hückel, deutscher Physiker und Theoretischer Chemiker, 1896-1980) soll zunächst in der einfachsten Form dargestellt werden. Für den wahrhaft Interessierten sei auf das Acrolein-Molekül verwiesen.

Wir kennen bereits die LCAO-Näherung, nach der in der allgemeinen Form gilt:
 

Σkck(Hik - E · Sik)  =  0

Wir machen nun die grobe Näherung Sik = δik, d.h. das Überlappungsintegral zu den Nachbarn wird vernachlässigt, weiterhin setzen wir Hii = α, d.h. es werden nur gleiche Atome (Orbitale) betrachtet und Hik = β für i = k ±1 und Hik = 0 für andere i,k-Werte, d.h. nur die nächsten Nachbarn zum i-ten Atom tragen zur Bindung bei und die Wechselwirkung ist für alle beteiligten Atomorbitale gleich β.

Die Säkulargleichung, die sich aus der obigen allgemeinen Gleichung ergibt lautet dann für ein zweiatomiges Molekül:

(a - E) · c1 + β · c2  =  0
β · c1 + (a - E) · c2  =  0

Wir erhalten nur dann nichttriviale Lösungen (d.h. ci¹ 0), wenn die Säkulardeterminante verschwindet:

½a-E
b ½
½b
α-E½
 = 0
(aus Darstellungsgründen im HTML-Format wird im Folgenden die Determinante in Form einer Tabelle gezeigt). Division durch b und Abkürzen mit x = (α-E)/b ergibt:
 
x
1
1
x
 = 0

Auflösen, d.h. Multiplikation der Hauptdiagonalelemente minus Multiplikation der Nebendiagonalelemente ergibt:

x2-1 = 0  mit der Lösung  x1/2 = ± 1,

also E1 = a + b  und  E2 = a - b.

Im Fall von H2 erhalten wir danach beispielsweise für den niedrigsten Zustand, der doppelt besetzt ist, Etotal = 2(a + b).
Da die Energieabsenkung 2b = -0.174a.u. beträgt, folgt daraus b = -0.087a.u (= 228 kJ/mol).

Für das (einfach besetzte) H2+-Ion,  Etotal = a + b, erwarten wir danach eine Energieabsenkung von b = -0.087a.u.(= 228 kJ/mol), was recht gut mit dem wahren Wert von b = -0.10a.u. (= 262 kJ/mol) überein stimmt.
Für Ethen H2C=CH2 können wir bzgl. der π-Bindungen genauso vorgehen. Jedes C-Atom steuert gerade ein Elektron zum π-System bei, so dass wir für die totale Energie Etotal = 2a + 2b erhalten. Da bei einer Anregung p ® p* ein Elektron um 2β über den Grundzustand liegt, können wir für π-Bindungen b = -75 kJ/mol abschätzen und die Bindungsenergie kann vorausgesagt werden.

Für lineares H3+: H-H-H (die H-Atome sind von links nach rechts durchnumeriert) und für ringförmiges H3 lauten die Säkulardeterminanten:
lineares H3+ 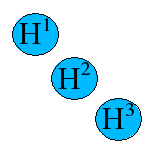ringförmiges H3+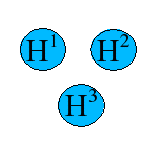
x 1 0
 = 0
1 x 1
0 1 x
x 1 1
 = 0
1 x 1
1 1 x
Ergebnisse
x1 = 0 E1 = α x1/2 = 1 E1/2 = α - β
x2/3 = ±√2 E2/3 = α ± β x3 = -2 E3 = α + 2β
Etotal = 2(α + β√2) = 2α + 2,83β Etotal = 2α + 4β
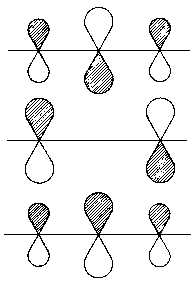Da b<0 ist, sollte H3+ als Ringmolekül vorliegen (kleinste Energie).


 
Abb.1:  Schematische Darstellung der Orbitale für die Energiewerte a+bÖ2 (energetisch niedrigster Wert, unten), α(Mitte), a-bÖ2 (energetisch höchster Wert, oben).
Das Allylanion (CH2=CH−CH2) können wir genauso wie das lineare H3+ behandeln, d.h. wir bekommen die Niveaus (in energetischer Reihenfolge): a+bÖ2, a, a-bÖ2. Die sich aus den π-Elektronen ergebenden Orbitale sind in der nebenstehenden Abb.1 schematisch dargestellt. Um sie zu erhalten, müssen wir die Eigenvektoren bestimmen. Die zu jedem xi gehörenden Eigenvektoren ci werden berechnet, indem wir einen Eigenwert in die Säkulargleichungen einsetzten. Wir erhalten zwei unabhängige Gleichungen (eine der drei Gleichungen ist linear abhängig). Es folgt ein Beispiel für den Eigenwert x2 = Ö2:
 
I Ö2·c1 + 1·c2 + 0·c3  =  0
II 1·c1 + Ö2·c2 + 1·c3  =  0
III 0·c1 + 1·c2 + Ö2·c3  =  0

Aus I folgt: c2 = -Ö2·c1
Einsetzen in II ergibt: c3  =  −c1-Ö2·c2  =  −c1 + 2·c1  =  c1
Wir erhalten also für das energetisch höchste Niveau:
 

π:
y  =  c1(φ1 - Ö2·φ2 + φ3)

Den letzen Koeffizienten c1 erhalten wir über die Normierung der Wellenfunktion, wobei wir beachten, dass  φi·φk = δik ist:

1  =  c1² (1² + Ö2² + 1²) Þ  c1  = 1/2

Die Säkulardeterminante von Butadien (C4H6, CH2=CH−CH=CH2) führt auf eine Gleichung vierten Grades, wenn wir die C-C-Bindungen betrachten:
 

1  2  3  4 
1  x  1  0  0 
2  1 x  1  0 
3  0  1  x  1
4 0  0  1  x 
Die Nullstellen dieser Gleichung sind:

 x1 = −½ - ½ Ö5 = −1,618
 x2 = +½ - ½ Ö5 = −0,618
 x3 = −½ + ½ Ö5 = +0,618
 x4 = +½ + ½ Ö5 = +1,618

Die Einelektronenergien der vier LCAO-MOs ergeben sich aus der Gleichung E = a - x β:
 

E1 = α + 1,618 β
E2 = α + 0,618 β
E3 = α − 0,618 β
E4 = α − 1,618 β

Wir müssen nun unsere 4 Elektronen unterbringen. Die Gesamtenergie des Moleküls ergibt sich als Summe der Energien der besetzten Orbitale. Für das Butadien-Molekül im Grundzustand beträgt die Elektronen-Gesamtenergie daher:

Etotal  =  2 (α + 1,618 β) + 2 (α + 0,618 β)  =  4α + 4,472 β

Vergleichen wir das Ergebnis mit zwei Ethenmolekülen, für die wir 2· (2α + 2β) = 4α + 4β erhielten, dann sehen wir, dass Butadien um 4,472 b - 4β = 0,472 β ≈ −35 kJ/mol stabiler ist.

Diese zusätzliche Stabilisierung des konjugierten Systems nennt man Delokalisierungsenergie.

Wir können also die energetische Verhältnisse vieler Systeme relativ leicht abschätzen. Um die Wellenfunktion für die so konstruierten Zustände zu erhalten, müssen wir die Eigenvektoren bestimmen. Die zu jedem xi gehörende Eigenvektoren ci werden wie folgt berechnet: Wir setzten einen Eigenwert in die Säkulargleichungen ein und erhalten drei unabhängige Gleichungen (eine der vier Gleichungen ist linear abhängig). Wir lösen diese in Abhängigkeit eines Koeffizienten, der zuletzt über die Normierung bestimmt wird. (Beispiel für den ersten Eigenwert x1 = 1,618).
 

I x1c1 + 1·c2 + 0·c3 + 0·c4  =  0
II 1·c1 + x1c2 + 1·c3 + 0·c4  =  0
III 0·c1 + 1·c2 + x1c3 + 1·c4  =  0
IV 0·c1 + 0·c2 + 1·c3 + x1c4  =  0

Aus I folgt: c2 = −x1c1 = 1,618 c1

Einsetzen in II ergibt:

c3  =  −c1− x1c2  =  −c1 + 1,618 · 1,618 c1  =  +1,618 c1

Einsetzen in III ergibt:

c4  =  −c2− x1c3  =  −1,618 c1 + 1,618 · 1,618 c1  =  c1
1π: y1  =  c1(φ1 + 1,618 φ2 + 1,618 φ3 + φ4)

wobei die φi die p-Orbitale von jedem C-Atom repräsentieren. Analog erhalten wir y2, y3, y4, indem wir x2, x3, x4 statt x1 in die Säkulargleichungen I - IV einsetzen:
 

2π: y2  =  c1(1,618 φ1 + φ2 - f3 − 1,618 φ4)
3π*: y3  =  c1(1,618 φ1 - f2 - f3 + 1,618 φ4)
4π*: y4  =  c1(φ1− 1,618 φ2 + 1,618 φ3 - f4)

Den letzen Koeffizienten c1 erhalten wir über die Normierung der Wellenfunktion, wobei wir beachten, dass  φi·φk = δik ist:

1  =  c1² (1,618² + 1² + 1² + 1,618²)

c1  =  0,372

Die Ergebnisse sind in der Tabelle zusammengestellt:
 

  MO 1 MO 2 
HOMO 		 MO 3 
LUMO 		 MO 4 
Eigenwerte  -1,618 -0,618 +0,618 +1,618 
Atom 1  +0,372 +0,601 +0,601 +0,372
Atom 2  +0,607 +0,372 -0,372 -0,601
Atom 3  +0,601 -0,372 -0,372 +0,601
Atom 4  +0,372 -0,601 +0,601 -0,372

4π* 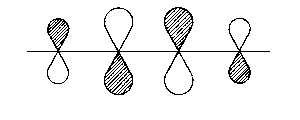überall antibindend
3π* 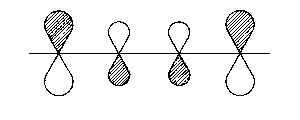1 - 2; 3 - 4 bindend
2 - 3 antibindend
2π 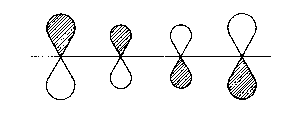1 - 2; 3 - 4 bindend
2 - 3 antibindend
1π 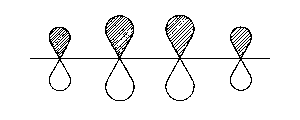überall (1-2-3-4) bindend
Abb. 2: Darstellung der Molekülorbitale, wie sich aus Hückels Behandlung des Butadien-Moleküls hervorgehen. Die schraffierten Flächen sollen Bereiche anzeigen, in welchen die Wellenfunktion ein positives Vorzeichen aufweist.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.