Linearkombination von Atomorbitalen (LCAO)

Dank des Doppelspaltexperiments kennen wir bereits ein wesentliches Prinzip der Quantenmechanik, nämlich dass sich die richtige Wahrscheinlichkeitsamplitude zur Beschreibung eines Systems als Linearkombination der Einzelamplituden darstellen läßt. Wir wollen nun molekulare Energiezustände und Wellenfunktionen bestimmen. Hierzu müssten wir die Schrödingergleichung Hy_n  =  E_n y_nlösen, wobei H der Hamiltonoperator für das Molekül ist und die y_nsind dann die Molekülorbitale. Zur Analyse des Systems entwickeln wir die Eigenfunktion y_n nach anderen (uns sehr wohl bekannten) Basisfunktionen φ_k, wobei die entsprechenden φ_k dann natürlich nicht mehr Eigenfunktion bzgl. Hy_n sind: y = Σ_k c_kφ_k (zur Vereinfachung ist der Index n weggelassen worden). Der nachfolgende Teil ist mathematisch abstrakt gehalten. Wer sich jedoch auf etwas einfachere Weise einen ersten prinzipiellen Eindruck verschaffen möchte, sollte hier klicken.
Die auffallendste Eigenschaft eines Molekülorbitals (MO)  ist die Mehrzentrigkeit. Dadurch unterscheidet es sich von einem Atomorbital (AO). Man beschreibt das Elektron physikalisch am besten, wenn man sagt, es bewege sich in einem Orbital, das die Umgebung beider (resp. aller) Kerne umfaßt. Wir wollen zur Beschreibung der Molekülorbitale y diese als Linearkombination von Atomorbitalen f darstellen (LCAO = Linear Combination of Atomic Orbitals). Welche f man am besten auswählt, werden wir bald sehen. Doch zunächst ist die Entwicklung der y-Funktion nach den φ's mit den üblichen Abkürzungen für den allgemeinen Fall (beliebiges Molekül) beliebig vieler φ-Funktionen in der linken Spalte, bzw. für ein zweiatomiges Molekül (mit nur 2 φ-Funktionen) in der rechten Spalte der Tabelle dargestellt:
 

Es handelt sich um lineare Gleichungssysteme (Säkulargleichungen), die nur dann eine andere als die mathematisch triviale Lösung c_k=0 haben, wenn die sogenannte Säkulardeterminante verschwindet. Im zweiatomigen Fall ist die Lösung auch einfacher zu erhalten. Wir brauchen beide Gleichungen nur nach c_A/c_B auflösen und gleichsetzen. Vielleicht irritiert es, dass überhaupt eine Größe òf_i*φ_kdτ auftaucht; haben wir doch gelernt, dass die f-Funktionen eines Atoms, also die AOs, orthogonal sind. Stimmt natuerlich, aber eben nur, wenn sie sich auf das gleiche Zentrum (Atom) beziehen. Bei Molekülen sind die AOs unterschiedlicher Atome aber wegen der Mehrzentrigkeit gegeneinander verschoben und da sind sie natürlich nicht zwangsläufig orthogonal. Wir ahnen aber schon, dass es sehr wünschenswert wäre zu wissen, wann das Integral  ò f_A*φ_Bdτ verschwindet. Wer ungeduldig ist und selber nachdenken möchte, kann schon einmal unterschiedliche Atomorbitale, z.B. 1s_A (für Atom A) mit 2p_x, 2p_y, oder 2p_z des Atoms B "paaren" und sich überlegen, wann das Integral verschwindet. Doch zunächst sei darauf hingewiesen, dass Größen wie H_AA, H_AB, S_AB etc. in allen Anwendungen der LCAO-MO-Theorie auftreten, und deshalb ist es wichtig, ihre physikalische Bedeutung genau zu kennen. Häufig wird auch eine andere Abkürzung gewählt:

Die Gleichungen für das AB-System lauten dann:

Wir wollen uns zunächst die Bedeutung der Größen verdeutlichen:  Unter der Annahme einer normierten Funktion φ_A stellt die Größe α_A etwa die Energie dar, die das Elektron haben würde, wenn es sich im Orbital φ_A am Atom A bewegen würde; eine analoge Interpretation gilt für α_B. Die Energie α_A ist nicht genau so groß wie E_A, die Energie eines Elektrons in φ_A am isolierten Kern A, denn H enthält auch einen anziehenden Term für den Kern B. α_A ist der Erwartungswert der Energie eines Elektrons, das durch φ_A beschrieben wird. Die Beiträge für α_A kommen hauptsächlich aus dem kernnahen Bereich von A, wo auch φ_A groß ist, und das ist genau der Bereich, in dem H dem Operator eines freien Atoms ähnlich ist. Demnach ist α_A (oder α_B) etwa die Energie eines Elektrons in φ_A (oder φ_B) am Atom A (oder B), die durch die Anwesenheit des zweiten Atoms geringfügig verändert wird. Die Größen α_A und α_B enthalten Coulomb-Wechselwirkungsterme und werden deshalb kurz Coulombintegrale genannt. Der Betrag der α-Werte steigt, wenn wir für einen bestimmten Orbitaltyp im Periodensystem von links nach rechts gehen. Von links nach rechts nimmt die Elektronegativität oder die "elektronenanziehende Wirkung" der Atome zu.

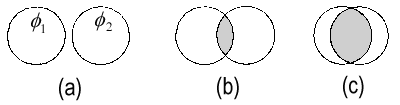Die Überlappung S12 zwischen zwei gleichen s-Orbitalen φ1 und φ2: (a) S12 ≈ 0; (b) S12 klein; (c) S12 → 1.

Die obigen Integrale hängen sowohl von φ_A als auch von φ_B ab. Es dürfte klar sein, dass β und S nur dann dem Betrag nach zu größeren Werten fähig sind, wenn sich beide Atomorbitale hinreichend stark überlappen. Wir nennen die Größe S Überlappungsintegral und die Größe β Bindungsintegral.
Die Lösung der Säkulargleichungen lautet für homonukleare Moleküle (bei denen das Atom A mit dem Atom B identisch ist, also α_A = α_B) etwas anders als für heteronukleare Moleküle (α_A ¹a_B), und deshalb werden wir die beiden Fälle gesondert behandeln. Um das Wesentliche zu verstehen, wenden wir uns zunächst dem einfachsten Molekül zu: Es ist das H₂⁺-Ion. Die Laborchemiker mögen nun enttäuscht sein, denn wo begegnet ihnen schon dieses Ion; doch auch sie können nur vom Einfachen her das Komplexe verstehen.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.