Homonukleare Moleküle A₂

Eine besonders einfache Form nimmt die LCAO-Entwicklung homonukleare zweiatomige Moleküle an; das sind Moleküle mit gleichen Atomen, wie beispielsweise H₂, O₂, N₂ usw. Unsere Erfahrungen, mit dem einfachsten dieser Systeme, dem Wasserstoffmolekül-Ion H₂⁺, lassen sich leicht auf andere homonuklearen Moleküle übertragen. Es kommen allerdings einige Besonderheiten hinzu, insbesondere dann, wenn mehr als ein Elektron an der Bindung beteiligt ist. Analog zu den Atomen wollen wir jedem Elektron im Molekül ein Orbital zuordnen und diese Molekülorbitale (MO) in der Reihenfolge zunehmender Energie mit Elektronen besetzen, wobei wir natürlich das Pauli-Prinzip beachten müssen. Wir stellen diese MOs in erster Näherung als Linearkombination von Atomorbitalen dar. Aus den 1s-Orbitalen der beteiligten Atome kann man zwei MOs aufbauen, so wie wir sie bereits beim H₂⁺-Ion kennengelernt haben:

wobei wir die (unterschiedliche) Normierungskonstante übersichtlichkeitshalber weggelassen und die neuen Wellenfunktionen mit dem griechischen Buchstaben σ (in Analogie zu s bei Atomen) versehen haben. Die Bedeutung der Indices wird spaeter erörtert. Wir beachten, dass in den Säkulargleichungen die Größen α_A und α_B bei homonuklearen Molekülen gleich sein müssen: α_A = α_B = a. Dies hat auch zur Folge, dass die beiden Wellenfunktionen mit dem gleichen Gewicht (aber eventuell unterschiedlichen Vorzeichen) eingehen.

Ein ursprünglich entartetes Paar von Energiewerten α spaltet also in zwei verschiedene Werte auf und zwar symmetrisch bzgl. des ursprünglichen Energiewertes, falls S, das Überlappungsintegral,  klein gegen 1 ist. Der eine neue Energiewert liegt dann höher und der andere niedriger als zuvor. Das MO mit der tieferen Energie ist das bindende MO, denn dessen Energie ist kleiner als die der getrennten Atome. Das andere MO mit der höheren Energie ist das antibindende MO; dessen Energie ist größer als die der getrennten Atome. Die Ergebnisse sind in der Abbildung schematisch dargestellt.
 

Wir besetzen nun die MOs in der energetischen Reihenfolge mit Elektronen unter Beachtung des Pauliprinzips. Für das H₂ erhalten wir dann die Wellenfunktion σ_g(1) für das eine Elektron und σ_g(2) für das andere Elektron. Die Gesamtwellenfunktion ist dann in unserem MO-Bild:

Die beiden ersten Terme geben an, dass sich die beiden Elektronen an unterschiedlichen Kernen (hier Protonen) aufhalten, während die beiden letzten Terme beschreiben, dass sich beide Elektron an einem Kern (A bzw. B) aufhalten. Ein anderer Ansatz von Heitler-London lässt einfach diese beiden letzten Terme weg, da sich die Elektronen gegenseitig abstoßen und daher nicht zu erwarten ist, dass sie sich beide am gleichen Kern aufhalten (d.h. es besteht eine Korrelation zwischen den beiden Elektronen). Gelegentlich tun sie es aber doch. Daher sind MO und Heitler-Londer zwei extreme Ansätze; die bessere Beschreibung der Molekülwellenfunktion wird dazwischen liegen. Z.B. im sogenannten ionischer Ansatz:

mit c als Variationskonstante.

1. Die Energiewerte von φ_A und φ_B in den entsprechenden getrennten Atomen A und B sollten möglichst ähnlich sein. Daraus folgt beispielsweise, dass die Valenzorbitale zweier Atome ausgesprochen stark miteinander kombinieren; im Gegensatz dazu gibt es aber keine nennenswerte Kombination zwischen Valenzorbitale und Orbitalen der inneren Schalen. Letztere liegen energetisch ausgesprochen tief.
2. Das Produkt φ_A·φ_B sollte möglichst groß sein, was häufig als "Prinzip der maximalen Überlappung" bezeichnet wird.
3. Die Funktionen φ_A und φ_B müssen bzgl. der Molekülachse die gleiche Symmetrie aufweisen.

Mögliche Kombinationen von Atomorbitalen vom s-Typ, p-Typ und d-Typ sind in der folgenden Tabelle aufgeführt:
 

Die Kombination von atomaren p-Orbitalen zu MOs ist in der nächsten Abbildung dargestellt (diverse MOs zum Anklicken: 1s+1s, 2s+2s, 2pz-2pz, 2pz+2pz, 2px+2px, 2px-2px). Die Negativkombination zweier p_z-Orbitale (der Konvetion entsprechend entspricht die z-Richtung der Kernverbindungsachse) führt zum bindenden Zustand σ_g, während die positive Linearkombination dieser p_z-Orbitale zum antibindenden σ_u führt. Sowohl die Kombination von p_x-als auch von p_y-Orbitalen ergibt π-Orbitale, die daher zweifach entartet sind. Die positive Linearkombination führt zu einer großen Überlappung und ergibt daher ein bindendes MO (π_u), während die negative Kombination zum antibindenden MO (π_g) führt.

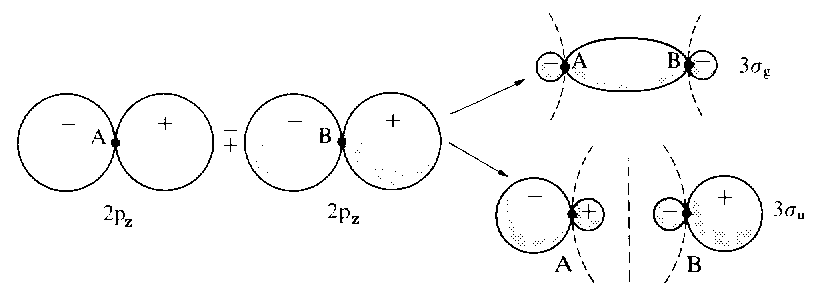Die Kombinationen von zwei 2pz-Atomorbitalen zur Erzeugung eines bindenden und eines antibinden Molekül- orbitals, symbolisiert durch 3σg und 3σu. Die z-Achse zeigt nach rechts; man beachte die Vorzeichen an den Lappen und wie diese kombinieren (die Negativkombination führt zum bindenden Zustand). Die Knotenflächen sind durch unterbrochenen Linien angedeutet.

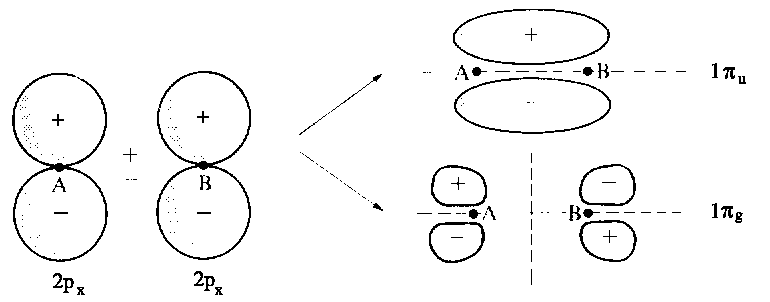Die Kombination von zwei 2px-Atomorbitalen zur Erzeugung eines bindenden und eines antibindenden Molekül- orbitals, symbolisiert durch 1πu und 1πg. Die x-Achse verläuft senkrecht zur Bindungsachse. Man beachte die Vorzeichen an den Lappen. Im Gegensatz zur Kombination zweier pz-Atomorbitalen führt eine positive Kombination  zum bindenden Zustand. Die Knotenfläche sind durch unterbrochene Linien angedeutet. πu und πg sind jeweils zweifach entartet, da das andere MO entsprechend  mit den 2py-AO konstruiert wird.

Die Symbole, die man zur Kennzeichnung der Molekülorbitale verwendet, besitzen eine gewisse Ähnlichkeit mit denjenigen für Atomorbitale. Die Symbole s, p, d,...bei den Atomen stehen im Zusammenhang mit σ, π, δ und beziehen sich auf den Drehimpuls der Elektronen bezgl. der Kernverbindungsachse und auf die Symmetrie des Molekülorbitals:

• ein σ-MO wie beim H₂⁺ bleibt bei der Symmetrieoperation einer Rotation um die Molekülachse immer unverändert, mit anderen Worten, es hat eine axiale Symmetrie;
• ein π-MO, das positive und negative Lappen hat, die durch eine Knotenebene voneinander getrennt sind, ändert bei einer Drehung von 180° um die Molekülachse das Vorzeichen;
• ein MO, das aus d_xy-Atomorbitalen an den Zentren A und B aufgebaut ist, hat zwei Knotenebenen, die das MO in vier Lappen unterteilen, und dadurch ändert sich das Vorzeichen des Molekülorbitals, wenn dieses um 90° gedreht wird; etc. für alphabetisch höhere griechische Buchstaben.

• ein σ-MO hat die Drehimpulskomponente l = 0 bezüglich der Kernverbindungsachse, also 0h;
• ein π-MO hat die Drehimpulskomponente l = 1, also 1h;
• ein δ-MO hat die Drehimpulskomponente l = 2, also 2h.

Die Zahlen 1, 2, 3, ... die vor dem Symmetriesymbol stehen, zählen die Molekülorbitale einer bestimmten Symmetrie in energetisch aufsteigender Reihenfolge.

Wollen wir wie im Fall der Atome auch für die Molekülstruktur ein Aufbauprinzip einführen, so müssen wir die energetische Reihenfolge der Molekül-Orbitale kennen. Nach heutigen Erkenntnissen lautet diese Reihenfolge
 

Bei zweiatomigen Molekülen mit Atomen aus der zweiten Reihe des Periodensystems liegt σ_g immer unterhalb von π_u. Es ist zu beachten, dass  jedes π-MO zweifach entartet ist, denn wir können z.B. unter dem 1π_u-MO das Paar 1π_xu und 1π_yu verstehen, das den Aufbau aus p_x- und p_y-AO deutlich macht.

Nun ist es relativ einfach, mit Hilfe des Aufbauprinzips zweiatomige Moleküle mit gleichen Kernen zu beschreiben (s. Tabelle). Die MOs besetzen wir im Sinne des Pauli-Prinzips mit Elektronen, wobei zu beachten ist, dass ein π-Niveau aufgrund der Entartung maximal 4 Elektronen aufnehmen kann. Wir haben bereits gesehen, dass H₂ die beiden Elektronen das bindende MO besetzten, so dass die Elektronenkonfiguration (1σ_g)² lautet. Gehen wir weiter zum He₂⁺, so hat dieses die Grundzustandskonfiguration (1σ_g)²(1σ_u); He₂ hätte die Konfiguration (1σ_g)²(1σ_u)². Tatsächlich ist He₂ im Grundzustand ein instabiles Molekül, während es in spektroskopisch beobachteten angeregten Zuständen, in denen ein Elektron sich in einem energetisch höher liegenden MO befindet, stabil ist (z.B. (1σ_g)²(1σ_u)(2σ_g)).

Die Instabilität von He₂ illustriert ein ziemlich allgemeines Prinzip: Sind ein bindendes MO und sein entsprechender antibindender "Partner" beide voll besetzt, so gibt es keine resultierende Bindung, ja sogar eine leicht überwiegende Antibindung (Abstoßung), da die Energieaufspaltung nicht völlig symmetrisch ist. Unter "Partnern" verstehen wir zwei Molekülorbitale, die aus demselben AO-Paar aufgebaut sind.

Für die inneren Schalen (mit sehr kleinen Werten für s) ist die MO-Beschreibung identisch mit der für die ungestörten Atome. Im allgemeinen werden die inneren Schalen durch die Buchstaben K, L, M, ... bezeichnet, so dass Li₂ mit zwei Valenzelektronen außerhalb der inneren Schalen entweder als

geschrieben werden kann, wobei KK die beiden ungestörten K-Schalen sind. Auf ähnliche Weise erhalten wir die Konfiguration für F₂

wobei (1π_u)⁴ das entartete Paar der doppelt besetzten Molekülorbitalen (1π_xu)²(1π_yu)² ist. Nun sind 2σ_g und 2σ_u bindende und antibindende Partner und ebenso 1π_u und 1π_g. Daraus folgt, dass von den 14 Valenzelektronen nur das (3σ_g)²-Paar zur Bindung beiträgt; somit ist die Einfachbindung vom σ-Typ erklärt.

Die Gesamtkonfiguration der Elektronen (Termsymbole) setzt sich aus den einzelnen Elektronenkonfigurationen zusammen. Details und eine Zusammenfassung der Notation gibt es durch Anklicken. Die Termsymbole werden durch große griechischen Buchstaben Σ, Π, Δ, ....(Projektion des Gesamtdrehimpulses auf die Kernverbindungsachse), einem tiefgestellen Index g oder u (bei Molekülen mit Symmetriezentrum) und einem vorgestellten hohen Index, der die Spinmultiplizität 2S+1 für den Gesamtspin S wiedergibt, gekennzeichnet. Der Vorzeichenindex ± bei Σ-Zuständen bezieht sich auf das Verhalten der Wellenfunktion bezüglich einer Spiegelung an einer beliebigen Ebene, die die Kerne enthält.

Beispiele:
²Π_u   Gesamtspin = 1/2; Gesamtdrehimpuls = 1; Wellenfkt. wechselt Vorzeichen bei Spiegelung am Symmetriezentrum.
³Σ_g^-  Gesamtspin = 1 ; Gesamtdrehimpuls = 0; Vorzeichen derWellenfkt. bei Spiegelung am Symmetriezentrum bleibt erhalten
 
 

Erstens: Die Begriffe Einfach-, Zweifach-, Dreifachbindung  beziehen sich auf die Anzahl der bindenden Elektronenpaare, die effektiv zur Bindung beitragen. Die Bindungsart hängt vom σ- oder π-Typ des Paares ab. Die charakteristischen Elektronenkonfigurationen lauten

Einfachbindung σ², Doppelbindung σ²π², Dreifachbindung σ²π⁴.

Für die Atome der ersten Reihe gibt es keine weiteren Bindungsarten, aber für Moleküle mit schweren Atomen gibt es auch noch andere Möglichkeiten. In einigen starken homonuklearen Metall-Metall-Bindungen kann es auch Vierfachbindungen mit der Konfiguration σ²π⁴δ² geben.

Zweitens: Das Prinzip der maximalen Überlappung besagt, dass π-Atomorbitale (senkrecht zur Bindung weniger überlappen als σ-Atomorbitale (parallel zur Bindung) und dass deshalb π-Bindungen schwächer als σ-Bindungen sind. Entsprechend sind antibindende σ-Orbitale stärker abstoßend als π-Orbitale.

Drittens: Beim Besetzten entarteter Orbitale (in diesem Fall ist es das π_x, π_y,-Paar) ist die Hundsche Regel wie beim Aufbauprinzip der Atome zu beachten. So sind beim O₂-Molekül alle Niveaus bis zu 1π_u hinauf voll besetzt und der parallele Spin in den entarteten 1π_g-Niveaus führt zu einem Triplett-Grundzustand (S = 1).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.