Auch bei heterogenen Molekülen gilt die qualitative Bedeutung der LCAO: Für eine erfolgreiche Kombination der Art y = cAφA + cBφB:
Die Bedingungen für einen wirksame Kombination von Atomorbitalen im LCAO-Ansatz können wir beispielsweise am Molekül HCl demonstrieren. Zunächst sagt uns die 1. Bedingung, die weiter unten mathematisch begründet wird und die eine vergleichbare Größe der Energiewerte fordert, dass die Atomorbitale 1s, 2s, 2p, 3s von Cl nicht wesentlich mit einem AO von H kombinieren werden, denn ihre Energien (mit der eventuellen Ausnahme von 3s) liegen viel zu tief. In der folgenden Gruppe haben wir beim Chloratom als einzige andere Möglichkeit die Orbitale 3px, 3py und 3pz. Nun ist das energetisch tiefste AO des Wasserstoffatoms das 1s-AO. Dieses kann, wie der Tabelle zu entnehmen ist, aus Symmetriegründen nur mit einem 3pz-AO kombinieren. Wie wir später sehen werden (Hybridisierung), beteiligt sich in geringem Maße auch noch das 3s-AO von Cl an dieser Kombination, aber dadurch ändert sich an der hier gegebenen Beschreibung nichts wesentliches. Aus dieser Diskussion, zusammen mit dem Aufbau-Prinzip, folgt für die Beschreibung des Grundzustandes des HCl-Moleküls
(1s)2 (2s)2 (2pz)2 (2px)2 (2py)2 (3s)2 (3px)2 (3py)2 {cAH(1s) + cBCl(3pz)}2
wobei die nicht gekennzeichneten Orbitale 1s, 2s, ... 3py
Atomorbitale am Cl-Atom sind. Diese nicht zur Bindung beitragenden Atomorbitale
werden dennoch nach ihrer Symmetrie klassifiziert, d.h. die s- und pz-Orbitale
werden σ und die px und py
werden π. Durch die Bindung rutscht das 5s
= {cAH(1s) + cBCl(3pz)} unter das
neutrale p-Atomorbital am Cl-Atom, das aus den
(3px)(3py) gebildet wird. Wir erhalten also nach
Durchnummerierung:
| (1σ)2 (2σ)2 (3σ)2 (1π)4 (4σ)2 (5σ)2 (2π)4 : 1Σ |
wobei (5σ) das bindende MO in der geschweiften Klammer ist, denn durch die Bindung rutscht das 5s = {cAH(1s) + cBCl(3pz)} unter das neutrale p-Atomorbital am Cl-Atom, das aus den (3px)(3py) gebildet wird.
Die Beziehung zwischen einem LCAO-MO eines Moleküls AB und seinen Komponenten, den Atomorbitalen φA und φB, hat noch eine besondere Bedeutung. Diese kommt am besten zum Ausdruck, wenn die beiden Elektronen, die das Molekülobital y = cAφA + cBφB besetzen, Valenzelektronen für die Bindung zwischen den Atomen A und B sind. Diese Elektronen werden gewöhnlich von beiden Atomen einzeln mitgebracht, und in diesen Atomen besetzen sie die Orbitale φA und φB. Auf diese Weise wird eine Beziehung hergestellt zwischen dem von zwei Elektronen besetzten MO und den beiden Atomorbitalen, in welche die beiden Elektronen erwartungsgemäß gehen würden, wenn die beiden Atome beliebig weit voneinander getrennt werden (auf die Problematik haben wir im Kapitel des Wasserstoffkations bereits hingewiesen). Man kann so etwa von dem Elektron sprechen, das ursprünglich im Zustand φA war, und dem im Zustand φB, und die dann als gepaarte Elektronen im Zustand y = cAφA + cBφB des Moleküls AB vorliegen. Wir können uns vorstellen, wie sich die beiden Atome A und B einander nähern, ohne dass eine Wechselwirkung eintritt und dann die geeigneten Elektronen in A und B miteinander paaren.
Schauen wir uns das Ganze etwas mathematischer an. Die Säkulargleichung für unsere heteronuklearen Moleküle AB
cA(αA−
E) + cB(β −
E·S) = 0
cA(β −
E·S) + cB(αB−
E) = 0
gibt nur dann eine relevante Lösung, wenn die Determinante verschwindet, d.h., wenn für die Energie E gilt:
(aA-E)(aB-E) - (b-ES)2 = 0
Die Lösung der quadratischen Gleichung bzgl. E ist sehr unübersichtlich. Das Wesentliche wird jedoch klar, wenn wir annehmen, dass die Energie des bindenden MO nahe bei der niedrigsten Energie der beiden AO-Energien liegt (Bedingung 1). Sagen wir ohne Beschränkung der Allgemeinheit, dies sei für A der Fall und damit können wir schreiben E » aA - DE, wobei DE die Energieverschiebung durch die Bindung repräsentiert.
Einsetzen (aA - aA + DE)(aB
- aA + DE) = (b - (aA - DE)S)2
Da DE << aA ist, folgt:
DE
·
(aB - aA) = (b - aAS)2
und damit unsere Bindungsenergie
DE = [b-aAS]2/[aB-aA].
Für die Energie des bindenden Zustandes erhalten wir daher:
| Ebindend = aA - [b - aAS]²/[aB - aA] |
Für das antibindende MO machen wir den Ansatz E » aB-DE
(aA - aB + DE)(aB - aB + DE) = (b-(aB - DE)S)2
Da DE << aB ist, folgt: (aA - aB) DE = (b - aBS)2 und damit unsere Abstoßungsenergie
DE = - [b - aBS]2/[aB - aA]
Für die Energie des antibindenden Zustandes erhalten wir daher:
| Eantibindend = aB + [b - aBS]²/[aB - aA] |
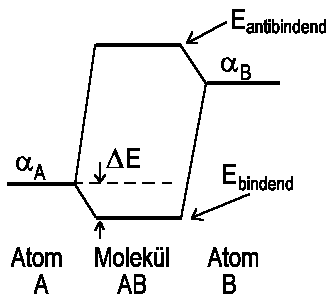 |
| Abb.1: In einem heteronuklearen Molekül neigt sich ein bindendes MO mehr zum elektronegativen Atom hin (hier A), wobei fA dominiert, während sich der entsprechend antibindende Partner mehr zum weniger elektronegativen Atom (hier B) neigt, wobei φB dominiert. |
Die sich daraus ergebenden Energieniveaus sind in Abb.1 dargestellt. Man erkennt am Nenner des Energieausdruck δ, dass die Energieaufspaltung um so geringer ist, je stärker die energeitsche Abweichung von αA und αB ist. Falls αA und αB nahezu gleich sind, dann gilt unsere obige Näherung nicht mehr, aber wir brauchen dann nur unter MOs für homonukleare Moleküle nachsehen, für die ja αA = αB gelten muss.
Um die Koeffizienten cA, cB - und damit die Beiträge der einzelnen AOs Orbitale - zu erhalten, setzen wir die Lösung (zunächst für das bindende MO) in die Gleichung (aA - E) cA + (b - ES) cB = 0 ein. Wiederum mit der Näherung E » aA - DE und DE << aA ergibt sich:
cA/cB = (b - aAS)/DE = - [aB - aA]/[b - aAS]
| ybindend = cA [fA+ [αAS - b]/[αB- aA] . fB] |
Die noch unbekannte Größe cA wird über die Normierung bestimmt.
Entsprechend erhalten wir für das antibindende MO:
cB/cA = [b - aBS]/[aB - aA]
| yantibindend = cA[fA- [αBS - b]/[αB- aA] . fB] |
Zur Illustration einer Linearkombination mit unterschiedlicher Wichtung
ist in der nachfolgenden Abb. 2 die Linearkombination eines fA=
2pz AO mit einem fB =
1s AO in Form eines 3D-Plots dargestellt, wobei cB/cA
= 3:7 gewählt wurde.
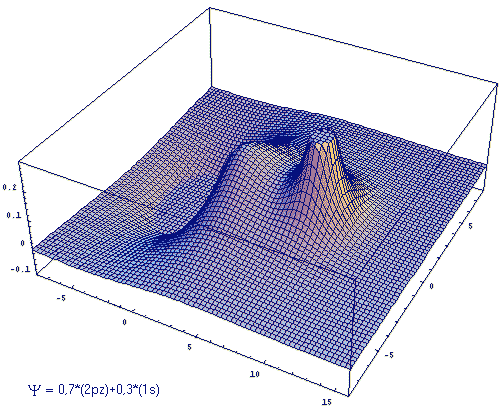 |
| Abb.2: Beispiel einer Linearkombination zweier AOs (2pz und 1s) mit unterschiedlicher Wichtung. |
Ein Korrelationsdiagramm zwischen den vollständig getrennten Atomen
und dem vereinten Atom ist für ein heteronukleares zweiatomiges
Molekül ( zum Vergleich homonukleare
Moleküle) in Abb.3 gezeigt. Als Symmetriesymbole treten
nur σ und π auf,
da die g-u-Klassifikation nur für homonukleare Moleküle in Erscheinung
treten kann. Zum besseren Verständnis zeigt Abb.4 einige Beispiele
der Korrelation zwischen Orbitalen des vereinigten Atoms und der getrennten
Atome.
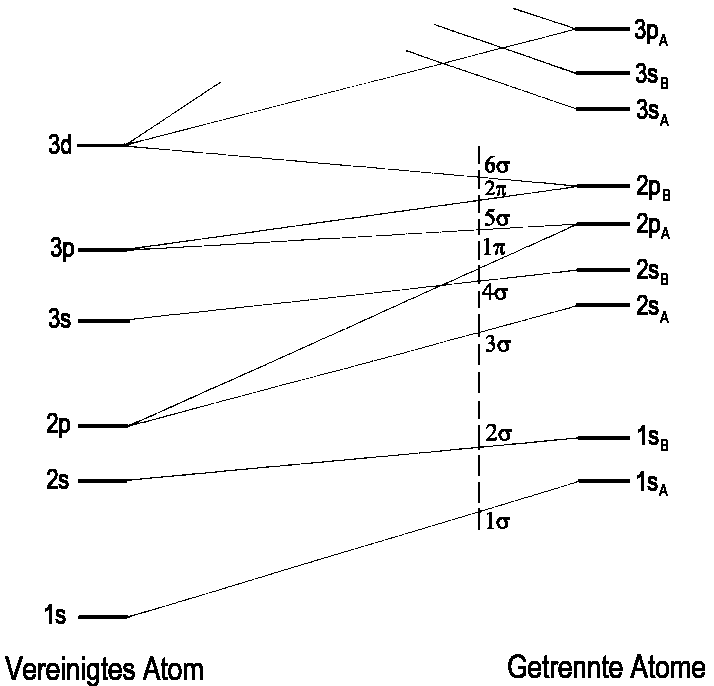 |
| Abb.3: Das Korrelationsdiagramm für ein heteronukleares zweiatomiges Molekül (vergl. Abb1. MO-Reihenfolge homonuklearer Moleküle). Als Symmetriesymbole treten nur σ und π auf, die g-u-Klassifikation tritt nicht mehr in Erscheinung Die vertikale unterbrochene Linie entspricht einer Sequenz von MO-Energien, wie sie im NO-Molekül auftreten. (Nach R.S. Mulliken, Rev. mod. Phys. 4, 1 (1932)). |
| 1s |  |
Û |  |
Û |  |
1sA |
| 2s |  |
Û | 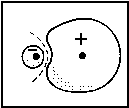 |
Û | 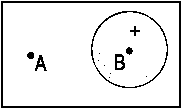 |
1sB |
| 2px |  |
Û |  |
Û |  |
2pxA |
| 3px |  |
Û |  |
Û |  |
2pxB |
| Vereinigtes Atom | Molekül | Getrennte Atome | ||||
| Abb.4: Beispiele der Korrelation zwischen Orbitalen des vereinigten Atoms und der getrennten Atome für ein heteronukleares zweiatomiges Molekül. Die Atomorbitale der getrennten Atome auf der rechten Seite liefern mit Hilfe einer bindenden und einer antibindenden Kombination je ein MO (in der Mitte) und schließlich die Atomorbitale des vereinigten Atoms (links). Man beachte, dass die antibindende Kombination durch die Erzeugung eines weiteren Knoten zu einem AO höherer Hauptquantenzahl führt. | ||||||
| Elektronische Konfiguration und Termsymbole der niedrigsten Zustände von XH | ||
| XH Molekül | Grundzustand | erster angeregter Zustand |
| LiH, BeH+
NaH, MgH+ CuH, ZnH+ |
K(2sσ)2:
1Σ+
KL(3sσ)2: 1Σ+ KLM(4sσ)2: 1Σ+ |
2sσ2pσ:
1Σ+
[3Σ+]
3sσ3pσ: 1Σ+ [3Σ+] 4sσ4pσ: 1Σ+ [3Σ+] |
| MgH, AlH+
CaH HgH |
KL(3sσ)2
3pσ: 2Σ+
KLMsp(4sσ)2 3dσ: 2Σ+ KLMNOspd(6sσ)2 6pσ: 2Σ+ |
(3sσ)2 3pπ:
2Πr
(4sσ)2 3dπ: 2Πr (6sσ)2 6pπ: 2Πr |
| BH, CH+ | K(2sσ)2 (2pσ)2: 1Σ+ | (2sσ)2 2pσ2pπ: 1Π, 3Π |
| CH | K(2sσ)2 (2pσ)2 2pπ: 2Πr | (2sσ)2 2pσ (2pπ)2: [4S-], 2Δ, 2Σ+, 2S- |
| NH, OH+ | K(2sσ)2 (2pσ)2 (2pπ)2: 3S-, 1Δ, 1Σ+ | (2sσ)2 2pσ (2pπ)3: 3Π, 1Π |
| OH | K(2sσ)2 (2pσ)2 (2pπ)3: 2Πi | (2sσ)2 2pσ (2pπ)4 : 2Σ+ |
| HF
HCl |
K(2sσ)2
(2pσ)2 (2pπ)4:
1Σ+
KL(3sσ)2 (3pσ)2 (3pπ)4 : 1Σ+ |
(2sσ)2 (2pσ)2
(2pπ)3 3sσ:
[3Π], [1Π]
(3sσ)2 (3pσ)2 (3pπ)3 4sσ: 3Π, 1Π |
| NiH | KLMsp(3dσ)2 (3dπ)4 (3dδ)3 (4sσ)2: 2Δ | (3dσ)2 (3dπ)4 (3dδ)3 4sσ4pσ: 2Δ, 2Δ, 4Δ |
| For the excited electron configurations the closed atomic shells have not been repeated. The states in brackets have not been observed. Msp means that in the M shell only the groups 3s and 3p are closed, and similarly in other case. | ||
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.