Hybridisierung

Wir wollen nun etwas genauer das Beispiel des Lithiumhydrids betrachten, wobei die LCAO-Darstellung der Molekülorbitale im Mittelpunkt stehen soll. Ab initio-SCF-Rechnungen mit minimaler Basis (als Li-Basis wird ein Satz der Wellenfunktionen Φ_1s, Φ _2s, Φ _2p bezeichnet, die H-Basis mit 1s erscheint im folgenden als Φ_H) führen nach Ransil (1960) zu den folgenden Molekülorbitalen (eine geringfügige Kombination von φ_1s mit den anderen Atomorbitalen wird vernachlässigt)

setzt sich somit aus der inneren Schale (1σ)² des Litiumatoms zusammen, die mit der im freien Atom nahezu identisch ist, sowie aus dem bindenden 2σ-MO, das zwei Elektronen enthält. Das Li-2p-AO ist zugelassen, denn es liegt nur geringfügig höher als das 2s-AO, und nach dem Energiekriterium gibt es keinen Grund, das 2p-AO auszuschließen. In der LCAO-Entwicklung sollten wir alle Atomorbitale mit nicht zu unterschiedlicher Energie miteinander kombinieren lassen und die Lösungen der Säkulargleichungen abwarten; genau diese Vorgangsweise (Methoden werden später beschrieben) führt zur obigen Gleichung.

Wir möchten an dem sehr einfachen Prinzip festhalten, wonach die Molekülorbitale für zweiatomige Moleküle aus überlappenden Paaren von Orbitalen, wobei sich an jedem Atom nur eines befindet, gebildet werden können. Das ist möglich, wenn die Gleichung in der Form

Die AO-Koeffizienten in dem Hybrid

sind mit einem gemeinsamen Faktor multipliziert worden, damit das Hybrid normiert ist. Ganz allgemein muss dafür die Bedingung

gelten (man beachte, dass die den Hybridorbitalen zugrundeliegenden Atomorbitale den Atomkern als gemeinsames Symmetriezentrum aufweisen und daher "gemischte" Integrale, wie ∫Φ_2sΦ_2pdτ  verschwinden). Zur Kennzeichnung eines solchen sp-Hybrids wird häufig die Population, d.h. a² und b², als hochgestellter Index verwendet: s⁰⁶⁶¹p^0.339 (a=0,813, a² = 0,661 und b= 0,582, b²=0,339). Immer häufiger wird auch auf s normiert: sp^0.51. Somit wird das bindende MO in LiH durch die Überlappung des H-1s-AO mit einem Li-Hybrid (h) gebildet (wobei der relative p-Anteil dem 0,51-fachen des s-Anteils entspricht):

Abb. 1: Niveaulinien für ein Hybridorbital, das aus einer s-p-Kombination gebildet wird. Die  Knotenebene (Nulldurchgang der Wellenfunktion, nahe der größten Konturlinie) ist durch  die Zumischung des s-Orbitals etwas vom Kern (bei 0,0) weggerückt.

Ein Hybridorbital ist also eine Linearkombination von Atomorbitalen eines einzelnen Atoms. Ein sp-Hybridorbital ist beispielsweise eine Funktion, die aus gleichen Anteilen von s- und p-Orbitalen desselben Atoms besteht (s. Abb.1). Ein Elektron, das dieses Orbital besetzt, hat dann 50% s-Charakter und 50% p-Charakter. In unserem Ausgangsbeispiel des Li-Hybrids war der 2s-Anteil etwas größer als der 2p-Anteil, er betrug 0,661:0,339 ≈ 1,95:1 statt 1:1 wie bei einer 50:50 Beteiligung. Ein sp³-Hybrid besitzt 25% s- und 75% p-Charakter (das bedeutet, dass s- und p-Orbitale im Verhältnis 1:3 beitragen). Ein sp³d²-Hybrid ist entsprechend ein Orbital, zu dem s-, p- und d-Funktionen im Verhältnis 1:3:2 beitragen.
Allgemein gilt, dass aus N Atomorbitalen N zueinander orthogonale Hybridorbitale konstruiert werden können. Was beruhigend ist, denn so geht uns kein Orbital durch die Hybridisierung verloren. Es gibt also
zwei orthogonale sp-Orbitale (Bilder sp-OrbitaleY, |Y|² als 3D und Konturplot)
drei orthogonale sp²-Hybride (Beispiele für sp²: Y, |Y|² als 3D und Konturplot)
vier orthogonale sp³-Hybride
und sechs sp³d²-Hybride.

Die Form der Hybridorbitale erhält man aus der Form der beitragenden Atomorbitale unter Beachtung der konstruktiven bzw. destruktiven Interferenz, die bei der Kombination auftritt. Die großen Lappen der sp-Hybridorbitale, die aus einem s- und einem p-Orbital gebildet werden können, zeigen in entgegengesetzte Richtungen. Der Winkel zwischen den Hybridorbitalen wird um so kleiner, je höher der p-Anteil ist. Die vier sp³-Hybride, die aus einem s.Orbital und einem Satz p-Orbitale entstehen, sind tetraedisch um as Atom angeordnet, und die sechs sp³d²-Orbitale bilden ein Oktaeder. Die Hybridorbitale werden stets so konstruiert, dass sie in Bindungsrichtung zeigen (bzw. in Raumrichtungen, die den Positionen von freien Elektronenpaaren entsprechen). Da alle hier erwähnten Hybridorbitale auch auch etwas s-Charakter besitzen, hat keins von ihnen eine Knotenfläche direkt am Ort des Kerns. Die Knotenflächen, die für p- und d-Orbitale typisch sind, sind in den Hybridorbitalen leicht vom Kern weg verschoben (Abb.1). Häufig vorkommende Hybridisierungen und die geometrische Anordnung der zugehörigen Hybridorbitale sind in der Tabelle abgegeben.
 

Hybridorbitale wurden ursprünglich im Rahmen der Valenzbildungstheorie eingeführt, in der jede Bindung durch Überlappung je eines Orbitals zweier benachbarter Atome beschrieben wird. In dem tetraedischen Molekül CH₄ werden die C-H-Bindungen beispielsweise durch Überlappung je eines H 1s-Orbitals mit einem der vier sp³-Hybridorbitale am Kohlenstoff erklärt. Bei der Beschreibung des trigonal pyramidalen Moleküls NH₃ muss sich eines der vier Hybridorbitale von den anderen drei unterscheiden. Da der HNH-Winkel mit 107° kleiner als der Tetraderwinkel ist, müssen die Hybridorbitale, die die N-H-Bindung ausbilden, einen größeren p-Anteil aufweisen als ein sp³-Orbital. Zur Charakterisierung von Hybridorbitalen können die an einem Molekül identifizierten Winkel herangezogen werden. Zwischen dem Koeffizienten λ in einem sp^λ hybridisierten Atom und der Ausrichtung der Bindungen zu seinen Bindungspartnern gilt folgende Beziehung (hier am Beispiel des NH₃, wobei φ den Bindungswinkel HNH symbolisiert)

cos φ =  −1/λ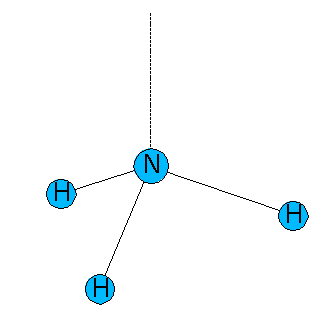

Für die die NH-Bindung eingehenden Hybridorbitale erhält man λ = 3,42, sie können als sp^3.42 Hybridorbitale beschrieben werden. Auch die Koeffizienten a und b der Linearkombination h  =  as + bp sind mit Hilfe des Bindungswinkels φ berechenbar (Zahlenwerte für NH₃)

a²  =  cos φ/cos φ −1	b²  =  1 - a²
a²  =  0,226	b²  =  0,774

Ebenfalls aus dem Winkel &phi ergibt sich die Hybridisierung weiterer vorhandener, nicht aber an Bindungen beteiligter Hybridorbitale. Im Falle von NH₃ nimmt das in der Molekülachse liegende Orbital das nichtbindende Elektronenpaar des N-Atoms auf. Da die Hybridorbitale der Bindung einen höheren p-Anteil haben, wird umgekehrt für dieses Orbital einen höherer s-Anteil aufweisen.

h'  =  a's + b'p'
a' 2 =  1 + cos φ/1 − cos φ
a' 2 =  0,71/1,29 =  0,547	⇒  b2 = 0,453
0,453 : 0,547 = 0,83	⇒ sp0,83-Hybridorbital

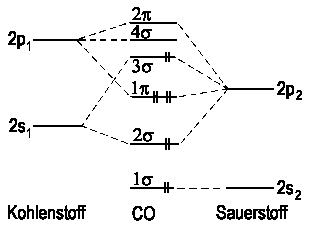Abb. 2a: Das Korrelationsdiagramm für das CO-Molekül ohne Hybridisierung. Das höchste besetzte MO (3σ) ist antibindend.

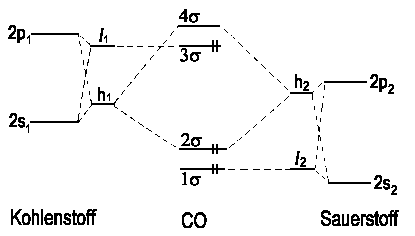Abb. 2b: Das Korrelationsdiagramm für das CO-Molekül mit Hybridisierung. Mit der verstärken Trennung der bindenden und antibindenden σ-MO wird das höchste besetzte MO (3σ) ein Orbital für ein einsames Elektronenpaar am Kohlenstoff, in Übereinstimmung mit dem Experiment. (Um die Übersichtlichkeit zu wahren, wurden die π-Niveaus weggelassen.)

Das CO-Molekül selbst ist ein ausgezeichnetes Besispiel für die Hybridisierung. Ohne Hybridisierung erhalten wir das Korrelationsdiagramm (nur für die Valenzelektronen) in Abb.2a paart man jene Atomorbitale, die sich energetisch am nächsten sind, so ist das niedrigste σ-MO im wesentlichen das O-2s-AO, ein einsames Elektronenpaar am Sauerstoff; die nächsten sechs Valenzelektronen werden durch (2σ)²(1π)⁴ (eine σ-Bindung und zwei π-Bindungen) beschrieben; schließlich ist (3σ)² ein Elektronenpaar in einem antibindenden σ-MO. Diese Beschreibung steht im Widerspruch zu den experimentellen Befunden, die auf eine starke σ-Bindung und auf ein einsames Paar am Kohlenstoff hindeuten. Der Effekt einer 2s-2p_z-Kombination (das 2p_z-AO hat σ-Symmetrie) ist in Abb.2b dargestellt. Der geringe energetische Unterschied zwischen h₁ (im wesentlichen C-2s) und h₂ (im wesentlichen O-2p), zusammen mit deren verstärkter Überlappung, liefert eine stark vergrößerte Aufspaltung zwischen den bindenden und den antibindenden Niveaus. Das 3σ-MO ist im wesentlichen das Kohlenstofforbital l₁, das ein Hybrid für ein einsames Elektronenpaar ist, das im wesentlichen aus dem 2p-AO besteht, aber mit etwas 2s-Charakter. Das antibindende MO ist nun unbesetzt, die am höchsten gelegenen zwei Elektronen sind im wesenltichen durch (l₁)² beschrieben; darüberhinaus zeigt h₁ in die Bindung hinein, und deshalb muss das zweite Hybrid l₁ aus der Bindung herauszeigen. Der orthogonale Partner von h₁ = a 2s + b 2p lautet l₁ = b 2s − a 2p.

Im einzelnen wird die CO-Gruppe sehr leicht an Übergangsmetallionen gebunden., wobei das elektronenreiche Kohlenstoffende durch das positive Ion angezogen wird. Die Gruppen CN⁻ und NO⁺ sind zu CO isoelektronisch und treten ebenfalls häufig in Übergangsmetallkomplexen auf, wobei die Bindung auf ähnliche Weise zu erklären ist.

Zusammenfassend kann festgestellt werden, dass das Konzept der Hybridisierung in der qualitativen Bindungstheorie von großer Bedeutung ist. Dieses Konzept liefert uns im Vorhinein die wichtigsten Ergebnisse einer vollständigen wellenmechanischen Berechnung: Die Paarung der Orbitale mit vergleichbaren Energien und eine ausreichende Überlappung .

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.