Klassifizierung der Moleküle
nach der Symmetrie

Alle an einem Molekül ausführbaren Symmetrieoperationen wird
als Symmetriepunktgruppe bezeichnet. Jedes Molekül gehört dabei
nur einer einzigen Symmetriepunktgruppe an. Die Symmetriepunktgruppen,
denen wirkliche Moleküle angehören, sind zwar recht zahlreich,
doch lassen sie sich systematisch einteilen, wenn man betrachtet, wie sie
aus zunehmend komplizierteren Kombinationen von Symmetrieoperationen aufgebaut
werden. Um die Moleküle nach ihrer Symmetrie zu klassifizieren, listet
man alle Symmetrieelemente eines Moleküls auf und schreibt Moleküle,
deren Listen übereinstimmen, in die gleiche Gruppe.
Es gibt zwei verschiedene Systeme zur Bezeichnung von Symmetriegruppen
(es ist also ein rein semantisches Problem, um zwischen beiden Bezeichnungen
zu wechseln); beide orientieren sich an den Symmetrieelementen, die die
Gruppe enthält:
Für Moleküle verwendet man in der Regel das System
von Schönflies (Arthur
Moritz, 17.4.1853 - 27.5.1928).
Das Hermann-Mauguinsche System (auch Internationales
System genannt) ist bei der Behandlung der Symmetrie der Kristalle
üblich.
Systematik von Symmetriepunktgruppen
-
Die Gruppen C1, Ci und Cs. Ein
Molekül gehört zu C1, wenn es außer der Identität
kein anderes Element enthält. Es kann erst durch eine 360°-Drehung
um eine beliebig hindurchgelegte Achse wieder zur Deckung gebracht werden.
Das aber ist identisch mit der Ausgangslage. (Diese "Symmetrie" besitzt
natürlich jede noch so "unsymmetrische" geometrische Figur.) Enthält
es neben der Identität noch die Inversion, gehört es zu Ci.
Wenn es außer der Identität noch eine Symmetrieebene besitzt,
gehört es zu Cs.
-
Die Gruppen Cn. Ein Molekül gehört zu Cn,
wenn es die Identität und eine n-zählige Achse besitzt.
(Cn hat drei Bedeutungen: es kann für ein Symmetrieelement,
eine Symmetrieoperation oder eine Gruppe stehen.)
-
Die Gruppen Cnv. Körper in diesen Gruppen besitzen
als Symmetrieelemente die Identität, eine Cn-Achse und
n
vertikale Symmetrieebenen.
-
Die Gruppen Cnh. Körper in dieser Gruppe haben als
Symmetrieelemente eine n-zählige Hauptachse und eine horizontale
Symmetrieebene. Oft folgt aus der Anwesenheit bestimmter Symmetrieelemente,
dass auch gewisse andere vorhanden sein müssen; in diesem Fall
muss die Inversion i ein Element der Gruppe sein, weil C2
und σh vorhanden sind.
-
Die Gruppen Dn. Die Moleküle dieser Gruppe haben
eine n-zählige Hauptachse und n zweizählige Achsen
senkrecht zu Cn.
-
Die Gruppen Dnh. Moleküle, die zusätzlich zu
den Elementen der Gruppe Dn eine horizontale Symmetrieebene
haben, bilden die Gruppe Dnh. Alle homonuklearen zweiatomigen
Moleküle gehören zur Gruppe D∞h,
und alle heteronuklearen Moleküle gehören zur Gruppe C∞v.
-
Die Gruppen Dnd. Moleküle, die zusätzlich zu
den Elementen der Gruppe Dn n diagonale Symmetrieebene
haben, bilden die Gruppe Dnd.
-
Die Gruppen Sn. Körper mit einer Drehspiegelachse
Sn gehören zur Gruppe Sn. Es gibt in Sn
nur sehr wenige Moleküle mit n>4.
Die Gruppe S2 ist identisch mit Ci.
-
Die kubischen Gruppen. Einige sehr wichtige Moleküle (z.B.
CH4) haben mehr als eine Hauptachse und gehören zu den
kubischen Gruppen, vor allem zu den Tetraeder-Gruppen T, Td,
Th und den Oktaeder-Gruppen O und Oh. Die Gruppe
Td ist die Gruppe des regelmäßigen Tetraeders, Oh
die des regelmäßigen Oktaeders. Wenn ein Körper zwar die
Rotationssymmetrie des Tetraeders bzw. Oktaeders hat, aber nicht die Symmetrieebenen
dieser Körper, dann gehört er zu den einfacheren Gruppen T bzw.
O. Die Gruppe Th enthält neben den Elementen von T noch
ein Inversionszentrum i.
-
Die Rotationsgruppe R3. Zu dieser Gruppe gehören
Kugel und ein einzelnes Atom, aber kein Molekül. Diese Gruppe spielt
eine wichtige Rolle, wenn man an Atomen Symmetrieüberlegungen anstellt.
Ein Flußdiagramm hilft Ihnen den
Überblick zu behalten.
Beispiele:
| Wasser |
|
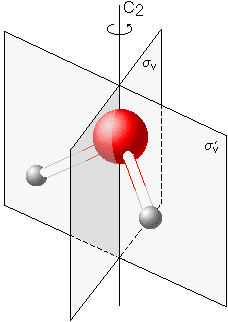 |
Das Wassermolekül besitzt eine 2-zählige Drehachse C2
und 2 zur Achse parallele Spiegelebenen σv
und σ'v und gehört damit zur
Symmetriepunktgruppe C2v. |
| trans-Butadien |
|
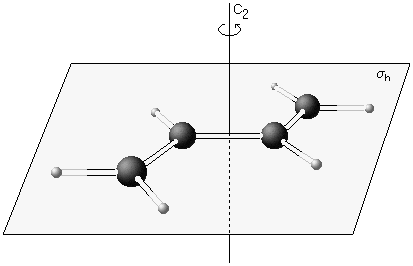 |
Das Butadienmolekül besitzt ein Inversionszentrum i, eine
2-zählige Drehachse C2 und eine horizontale (zur Achse
senkrechte) Spiegelebene
σh und gehört
zur Symmetriepunktgruppe C2h. |
| Benzol |
|
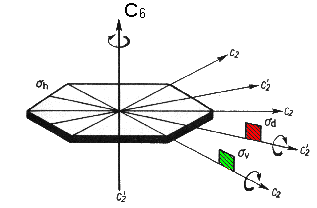 |
Das Benzolmolekül besitzt ein Inversionszentrum i,
Drehachsen C2, C2', eine 6-zählige Drehachse C6, und eine horizontale (zur C6
Achse
senkrechte) Spiegelebene
σh und zur
Achse parallele Spiegelebenen σv
und σd (jeweils 3) und gehörtzur
Symmetriepunktgruppe D6h. . |

 Inhalt
Inhalt
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.



![]()