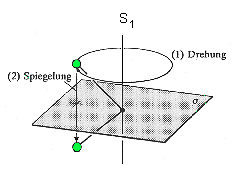
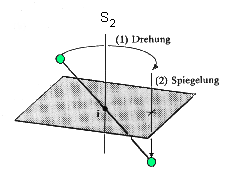
Eine weitere Möglichkeit einen Körper mit sich selbst zur
Deckung zu bringen, besteht in der Drehung um einen Winkel von 360°
/n und anschließender Spiegelung an einer Ebene senkrecht zur Drehachse.
Primäre Spiegelung und anschließende Drehung führt zum
selben Ergebnis. Diese Symmetrieoperation wird Drehspiegelung genannt und
mit dem Symbol Sn bezeichnet. Die Drehachse nennt man
Drehspiegelachse n-ter Ordnung und bezeichnet sie gleichfalls mit Sn.
Drehachse und Spiegelebene brauchen keine unabhängig voneinander wirksamen
echten Symmetrieelemente zu sein.
Es gibt nur Sn - Achsen mit n = 1 und n = 2, 4, 6,
... .
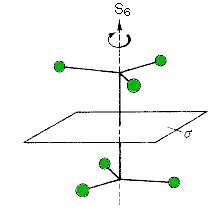
Sechszählige Drehspiegelachse S6
Beispiel 1: Drehspiegelung S4 im CH4-Molekül
(Movie, 1,2 Mb)
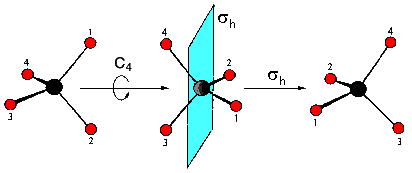
Beispiel 2: SiF4
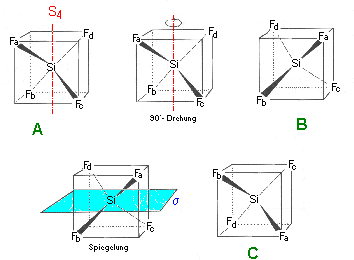
SiF4 besitzt zwar vier C3-Achsen, aber
keine C4-Achse. Es besitzt jedoch eine vierzählige
Drehspiegelachse
S4 .
Beispiel 3: trans-1,2 Dichlorethen
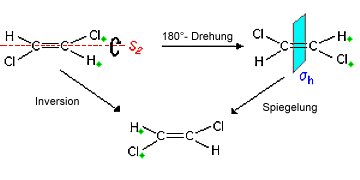
Wenn man das Molekül des trans-1,2 Dichlorethen um 180° um die C-C-Achse dreht und anschließend an der dazu senkrechten Ebene spiegelt, hat man eine erfolgreiche Drehspiegelung durchgeführt. Die S2-Achse verläuft durch die C-Atome. Beachtenswert ist hierbei, dass eine Inversion dasselbe Resultat ergibt. Die Symmetrieelemente S2 und i sind also äquivalent. In diesem Zusammenhang sei ergänzt, dass auch S1 und σ einander entsprechen, denn da C1 und E äquivalent sind, muss die als zweiter Schritt folgende Spiegelung, notwendigerweise s entsprechen. Eine Systematisierung zeigt dabei folgende Beziehungen:
i = S2 ; E = C1 ; s = S1.
Moleküle mit einer Drehspiegelachse zweiter Ordnung haben stets auch ein Symmetriezentrum, das im Schnittpunkt der S2-Achse mit der σh-Ebene liegt: i º S2 = C2σh .
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.