Hückel

First, we want to demonstrate the most simple manner of how Hückel (Erich Hückel, German physicist and theoretical chemist, 1896-1980) calculated molecular orbitals. Anyone truely interested in the method is invited to study Hückel's treatment of the acrolein molecule. We are already familiar with the LCAO approximation. It states, in general:

Σkck(Hik - E · Sik)  =  0

We now

• replace S_ik by δ_ik, i.e., ignore the overlap to the neighbours.
• use α instead of H_ii, i.e., only identical atoms (orbitals) are considered
• set H_ik = β for i = k ±1 and H_ik = 0 for any other pair of indices. Thus, only the neighbours of the i^th atom contribute to bonding and β represents the interaction found for each involved atomic orbital

In consequence, we employ the following secular equation to describe a diatomic molecule:

(α - E) · c₁ + β · c₂  =  0
β · c₁ + (α - E) · c₂  =  0

We only recieve non trivial (i.e. c_i≠0) solutions in cases where the secular determinant becomes zero:

	α-E	β		= 0
	β	α-E

Division by β and denoting (α-E)/β as x yields

	x	1		= 0
	1	x

The determinant is resolved (multiplication of the elements in both diagonals, subtraction of the product obtained in the secondary diagonal from the product in obtained in the main diagonal)

In the case of the molecule H₂, we obtain E_total = 2 (α+β) as state of minimal energy. Two electrons are within this state. The measured reduction of energy in the molecule H₂ is E = − 0.174 a.u.. According to the mathematical treatment presented here, this equals 2β, therefore β = − 0.087 a.u. or 228 kilojoule per mol.

For the H₂⁺ ion, E_total = α + β, we expect an energy reduction of β = -0.087 a.u., a value that agrees with the measured -0.10 a.u. or 262 kilojoule per mol.

In analogy, the π-bond in ethen H₂C=CH₂ is to be described. Each carbon atom contributes one electron to the π-system, therefore a total energy of E_total = 2α + 2β is obtained. In the excited state π → π* of ethen, one electron is 2β above the ground state. Together with spectroscopic measurements, these considerations lead to β = -75 kJ/mol, a value that, in turn, allows to predict the bonding energy.

For the cation H₃⁺, we get the following secular determinants and energy terms:

linear H3+		circular H3+
	x 1 0  = 0 1 x 1 0 1 x		x 1 1  = 0 1 x 1 1 1 x
Solutions
x1 = 0	E1 = α	x1/2 = 1	E1/2 = α - β
x2/3 = ±√2	E2/3 = α ± β	x3 = -2	E3 = α + 2β
	Etotal = 2(α + β√2) = 2α + 2.83β		Etotal = 2α + 4β

As β < 0, we expect H₃⁺ to form as circular molecule.

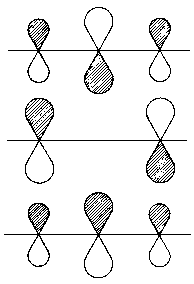Fig. 1:  Representation of the orbitals related the energy value α+b√2 (above, highest energy), α (middle) and α-β√2 (below, lowest energy).

We are able to treat the allyl anion (CH₂=CH-CH₂) in the same way as the linear H₃⁺ before. In the order of increasing energy, we get the levels α+β√2, α and α-β√2. The orbitals occupied by the former p-electrons are depicted in Fig. 1. To decribe these orbitals mathematically, we need to determine the eigenvectors. To any solution x_i of the secular equation, there is an eigenvector c_i. The components of this vector are calculated by insertion of one eigenvalue x_i (e.g. x₂=√2) into the secular equation. This yields two linear independent (and one linear dependent) equations

I	√2·c1 + 1·c2 + 0·c3  =  0
II	1·c1 + √2·c2 + 1·c3  =  0
III	0·c1 + 1·c2 + √2·c3  =  0

Equation I establishes the relation c₂ = -√2·c₁. Inserted in equation II, we get c₃  =  −c₁−√2·c₂  =  −c₁ + 2·c₁  =  c₁. Thus, for the highest energy level, we find the orbital
 

π:	Ψ  =  c1 (Φ1 - √2·Φ2 + Φ3)

Normalization of the wave function yields the value of the coefficient c₁. Note that Φ_i·Φ_k = δ_ik:

1  =  c₁² (1² + √2² + 1²) ⇒ c₁  = ¹/₂

The secular determinant of butadien (C₄H₆, CH₂=CH−CH=CH₂) leads to an equation of the forth degree. The zeros of this equation are:

x 1 0 0 1 x 1 0 0 1 x 1 0 0 1 x

The zeros of this equation are:  x1 = − ½ − ½ √5 = −1.618  x2 = + ½ − ½ √5 = −0.618  x3 = − ½ + ½ √5 = +0.618  x4 = + ½ + ½ √5 = +1.618

The single electron energies of the four LCAO molecular orbitals result from equation E = α - x β

E1 = α + 1.618 β E2 = α + 0.618 β E3 = α − 0.618 β E4 = α − 1.618 β

Four electrons need to be placed. The total energy of the molecule in the ground state is the sum of orbital energies occupied by electrons:

E_total = 2 (α + 1.618β) + 2 (α + 0.618β) = 4α + 4.472 β

If we compare this result with the 2·(2α + 2β) for two ethen molecules, we come to the conclusion that the energy of butadien is by an amount of [4α-4.472 β] - [4α+4β] = 0.472 β below the energy of two π-bonds. An energy difference of this kind, between a description with located conjugated π-bonds and molecular orbitals obtained in an approach like Hueckel's is called delocalization energy.

Now we are able to estimate the energies of many systems quite easily. To obtain the respective wave functions, we determine the eigenvectors. To each solution x_i of the secular equation, there is an eigenvector c_i which is calculated as follows: We insert the eigenvalue x_i into the secular equation and recieve three independent equations (one of the four is linear dependent ). We solve this system of equations. The value for the last coefficient emerges when the wave function is normalized. The method is exemplified for the first eigenvalue x₁ = 1.618).
 

I	x1c1 + 1·c2 + 0·c3 + 0·c4  =  0
II	1·c1 + x1c2 + 1·c3 + 0·c4  =  0
III	0·c1 + 1·c2 + x1c3 + 1·c4  =  0
IV	0·c1 + 0·c2 + 1·c3 + x1c4  =  0

Equation I states:

c₂ = −x₁c₁ = 1.618 c₁

Inserted in equation II:

c₃  =  −c₁− x₁c₂  =  −c₁ + 1.618 · 1.618 c₁  =  +1.618 c₁

Inserted in equation III:

c₄  =  −c₂− x₁c₃  =  −1.618 c₁ + 1.618 · 1.618 c₁  =  c₁

The wave function 1π of the respective molecular orbital is a linear combination of the four p-orbitals Φ of the carbon atoms. In an analogous way, the wave functions for orbitals of higher energy Ψ₂, Ψ₃ and Ψ₄ are recieved by inserting the eigenvalues into the secular equations.

1π:	Ψ1  =  c1(Φ1 + 1.618Φ2 + 1.618Φ3 + Φ4)
2π:	Ψ2  =  c1(1.618Φ1 + Φ2 − Φ3 − 1.618Φ4)
3π*:	Ψ3  =  c1(1.618Φ1 − Φ2 − Φ3 + 1.618Φ4)
4π*:	Ψ4  =  c1(Φ1− 1.618Φ2 + 1.618Φ3 − Φ4)

Again, normalization yields coefficient c₁. Note that Φ_i·Φ_k = δ_ik:

1  =  c₁² (1.618² + 1² + 1² + 1.618²)
c₁  =  0.372

The following table provides an overview on the recieved coefficients for the butadien molecule for the four eigenvalues. The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) are denoted.

	MO 1	MO 2  HOMO	MO 3  LUMO	MO 4
eigenvalue	-1.618	-0.618	+0.618	+1.618
atom 1	+0.372	+0.601	+0.601	+0.372
atom 2	+0.607	+0.372	-0.372	-0.601
atom 3	+0.601	-0.372	-0.372	+0.601
atom 4	+0.372	-0.601	+0.601	-0.372

4π*		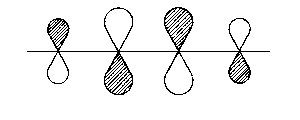throughout antibonding
3π*		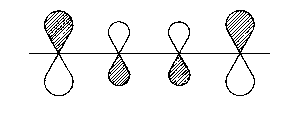1 - 2; 3 - 4 bonding 2 - 3 antibonding
2π		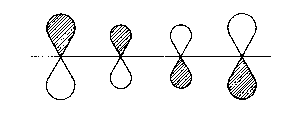1 - 2; 3 - 4 bonding 2 - 3 antibonding
1π		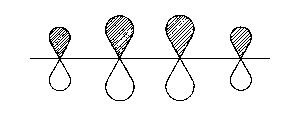throughout (1-2-3-4) bonding
Fig. 2: Representation of the molecular orbitals obtained with Hueckel's approach to the butadien molecule. The hatched area shall represent positive values of the wave function

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.